Câu hỏi:
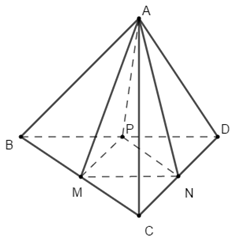
Cho tứ diện \(ABCD\) có các cạnh \(AB\), \(AC\), \(AD\) đôi một vuông góc với nhau. \(AB = 6a\), \(AC = 7a\), \(AD = 12a\). Gọi \(M,\,\,N,\,\,P\) tương ứng là trung điểm của các cạnh \(BC,\,\,CD,\,\,BD\). Tính thể tích của khối tứ diện \(AMNP\).
- A \(V = 21{a^3}.\)
- B \(V = \frac{{21}}{4}{a^3}.\)
- C \(V = 56{a^3}.\)
- D \(V = 7{a^3}.\)
Phương pháp giải:
Tính chiều cao của hình chóp.
Tính diện tính đáy hình chóp rồi thể tích hình chóp ABCD.
Dựa vào tỉ số thể tích để tính thể tích hình chóp AMNP.
Lời giải chi tiết:
Gọi \(h\) là độ dài đường cao của hình chóp.
Ta có \(AB,\,\,AC,\,\,AD\) đôi một vuông góc nên
\(\frac{1}{{{h^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{36}} + \frac{1}{{49}} + \frac{1}{{144}} \Rightarrow h = \sqrt {\frac{{7056}}{{389}}} \)
Áp dụng định lí Pytago vào các tam giác vuông \(ABC\), \(ACD\), \(ABD\) ta có:
\(BC = \sqrt {85} ;\,\,\,BD = 6\sqrt 5 ;\,\,\,CD = \sqrt {193} \)
\(\begin{array}{l} \Rightarrow \cos \angle CBD = \frac{{B{C^2} + B{D^2} - C{D^2}}}{{2BC.BD}} = \frac{{6\sqrt {17} }}{{85}}\\ \Rightarrow \sin \angle CBD = \sqrt {\frac{{389}}{{425}}} \\ \Rightarrow {S_{BCD}} = \frac{1}{2}.BC.DB.\sin \angle CBD\\{S_{MNP}} = \frac{1}{4}{S_{BCD}} = \frac{1}{8}.BC.BD.\sin \angle CBD\\ \Rightarrow {V_{MNP}} = \frac{1}{3}.h.{S_{MNP}} = 21{a^3}\end{array}\)
Chọn A.