Phương pháp giải:

Lời giải chi tiết:

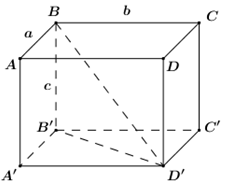
Gọi hình chữ nhật có kích thước như hình vẽ.

Ta có: \(\left\{ \begin{array}{l}{S_{tp}} = 2ab + 2bc + 2ca = 36\\BD' = \sqrt {BB{'^2} + B'D{'^2}}  = \sqrt {{a^2} + {b^2} + {c^2}}  = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}ab + bc + ca = 18\\{a^2} + {b^2} + {b^2} = 36\end{array} \right.\)

\(\begin{array}{l} \Rightarrow {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right) = 72\\ \Leftrightarrow {\left( {a + b + c} \right)^2} = 72 \Leftrightarrow a + b + c = 6\sqrt 2 \end{array}\)

Do \(a,\,\,b,\,\,c\) bình đẳng, không mất tính tổng quát ta giả sử \(a = \min \left\{ {a;b;} \right\} \Rightarrow a \le 2\sqrt 2 \).

Mặt khác

\(\begin{array}{l}ab + ac + bc = 18 \Rightarrow bc = 18 - a\left( {b + c} \right) = 18 - a\left( {6\sqrt 2  - a} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {a^2} - 6\sqrt 2 a + 18 = {\left( {a - 3\sqrt 2 } \right)^2}\end{array}\).

\(\begin{array}{l} \Rightarrow V = abc = a{\left( {a - 3\sqrt 2 } \right)^2} = \frac{1}{2}2a{\left( {3\sqrt 2  - a} \right)^2}\\\,\,\,\,\,\,\,\,\,\,\, \le \frac{1}{2}{\left[ {\frac{{2a + 3\sqrt 2  - a + 3\sqrt 2  - a}}{3}} \right]^3}\\\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}{\left( {2\sqrt 2 } \right)^3} = 8\sqrt 2 \end{array}\)

Vậy \({V_{\max }} = 8\sqrt 2  \Leftrightarrow 2a = 3\sqrt 2  - a \Leftrightarrow a = \sqrt 2 \).

Chọn B.