Phương pháp giải:

Sử dụng tính chất 2 đoạn thẳng song song để chứng minh góc bằng nhau.

Dùng tỉ số thể tích giữa các hình.

Lời giải chi tiết:

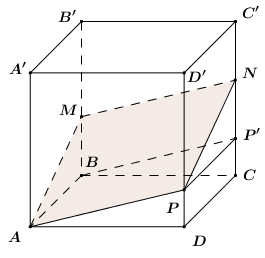
Ta có: \(\left\{ \begin{array}{l}\left( {AMNP} \right) \cap \left( {ABB'A'} \right) = AM\\\left( {AMNP} \right) \cap \left( {CDD'C'} \right) = NP\\\left( {ABB'A'} \right)\parallel \left( {CDD'C'} \right)\end{array} \right. \Rightarrow AM\parallel NP\).

CMTT ta có \(AP\parallel MN\).

\( \Rightarrow AMNP\) là hình bình hành \( \Rightarrow AM = PN\).

Trong \(\left( {CDD'C'} \right)\) kẻ \(PP'\parallel CD\,\,\left( {P' \in CC'} \right)\), ta có:

\(CDPP'\) là hình chữ nhật \( \Rightarrow PD = P'C \Rightarrow \Delta APD = \Delta BP'C\).

Xét \(\Delta ABM\) và \(\Delta PP'N\) có:

\(\begin{array}{l}AB = PP'\\AM = PN\\\angle MAB = \angle NPP'\,\,\left( {AM\parallel PN,\,\,AB\parallel PP'} \right)\end{array}\)

\( \Rightarrow \Delta ABM = \Delta PP'N\,\,\left( {c.g.c} \right)\)

\( \Rightarrow \)\(APD.BP'C,\,\,AMB.PNP'\) là hai khối lăng trụ.

Gọi cạnh của hình lập phương là 1, ta có: \({V_{ABCDMNP}} = \dfrac{1}{3}\).

Ta có: \({V_{ABCDMNP}} = {V_{APD.BP'C}} + {V_{AMB.PNP'}} = \dfrac{1}{3}\).

\(\begin{array}{l}{V_{APD.BP'C}} = CD.{S_{APD}} = CD.\dfrac{1}{2}.AD.PD = \dfrac{1}{2}PD\\{V_{AMB.PNP'}} = AD.{S_{PNP'}} = AD.\dfrac{1}{2}PP'.NP' = \dfrac{1}{2}NP'\end{array}\)

\( \Rightarrow \dfrac{1}{2}PD + \dfrac{1}{2}NP' = \dfrac{1}{3} \Leftrightarrow PD + NP' = \dfrac{2}{3} \Leftrightarrow P'C + NP' = \dfrac{2}{3} \Leftrightarrow CN = \dfrac{2}{3}\).

Vậy \(\dfrac{{CN}}{{CC'}} = \dfrac{2}{3}\).

Chọn D