Câu hỏi:
Cho một khối trụ có bán kính đường tròn đáy bằng \(10\). Cắt khối trụ bằng mặt phẳng \(\left( \alpha \right)\) song song với trục ta được thiết diện là hình chữ nhật \(ABCD\) sao cho \(A,\,\,B\) cùng thuộc một đáy của khối trụ và \(AB = 12\). Tính khoảng cách \(h\) từ trục của khối trụ đến mặt phẳng \(\left( \alpha \right)\).
- A \(h = 8\)
- B \(h = \sqrt {44} \)
- C \(h = 10\)
- D \(h = \sqrt {136} \)
Phương pháp giải:
Lời giải chi tiết:
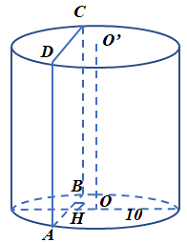
\( + \)Kẻ \(OH \bot AB\)(\(H\) là trung điểm \(AB\))
\( \Rightarrow \)Khoảng cách\(h\) từ trục \({\rm{OO}}'\) tới \(\left( \alpha \right)\)là \(OH\).
+ \(BH = \dfrac{{AB}}{2} = \dfrac{{12}}{2} = 6\)
\( + \) Xét \(\Delta OBH\) vuông tại \(H\) có:
\(O{H^2} = B{O^2} - H{B^2} \Leftrightarrow O{H^2} = {10^2} - {6^2} = 64 \Leftrightarrow OH = 8\)
Chọn A
Quảng cáo
Câu hỏi trước
