 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi:
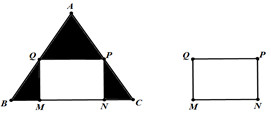
Cho một tấm nhôm hình tam giác đều có cạnh bằng \(20\left( {cm} \right)\). Người ta cắt ở ba góc của tấm nhôm đó ba tam giác như hình vẽ dưới đây để được hình chữ nhật MNPQ. Tìm độ dài đoạn MB để hình chữ nhật MNPQ có diện tích lớn nhất.
- A \(5\left( {cm} \right)\).
- B \(4\left( {cm} \right)\).
- C \(2\left( {cm} \right)\).
- D \(10\left( {cm} \right)\).
Phương pháp giải:
Lời giải chi tiết:
Ta có: \(MN = BC - 2BM = 20 - 2BM\)
Vì \(\Delta ABC\) đều \( \Rightarrow \widehat B = {60^\circ }\)
Xét \(\Delta BMQ\)vuông tại \(M\), có: \(\tan {60^0} = \dfrac{{QM}}{{BM}} \Rightarrow QM = BM.\sqrt 3 \)
\(\begin{array}{l}{S_{MNPQ}} = MN.QM = \left( {20 - 2BM} \right).BM\sqrt 3 = \underbrace { - 2\sqrt 3 .B{M^2} + 20\sqrt 3 .BM}_{f\left( x \right)}\\{S_{MNPQ\,}}max \Leftrightarrow f\left( x \right)\,max \Leftrightarrow BM = - \dfrac{b}{{2a}} = 5\,(cm)\end{array}\)
Chọn A.

















