Câu hỏi:
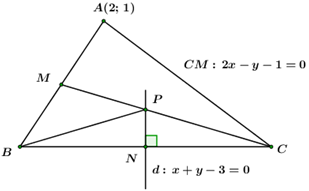
Trong mặt phẳng tọa độ \(Oxy,\) cho \(\Delta ABC\) có \(A(2;\,1),\) đường trung trực của đoạn \(BC\) và đường trung tuyến kẻ từ \(C\) có phương trình lần lượt là: \(x + y - 3 = 0,\,\,2x - y - 1 = 0.\) Khi đó tọa độ của đỉnh \(B,\,\,C\) là:
- A \(\left\{ \begin{array}{l}B\left( {0 ;\,\,1} \right)\\C\left( {2;\,\,3} \right)\end{array} \right.\)
- B \(\left\{ \begin{array}{l}B\left( {0 ;\, - \,1} \right)\\C\left( {2;\,\,3} \right)\end{array} \right.\)
- C \(\left\{ \begin{array}{l}B\left( {1 ;\,\,0} \right)\\C\left( {3;\,\,2} \right)\end{array} \right.\)
- D \(\left\{ \begin{array}{l}B\left( {0 ;\,\,1} \right)\\C\left( {3;\,\,2} \right)\end{array} \right.\)
Phương pháp giải:
Sử dụng tính chất đường trung trực và đường trung tuyến để làm bài toán.
Lời giải chi tiết:
Gọi \(N\) là trung điểm của \(BC \Rightarrow N \in d:\,\,x + y - 3 = 0 \Rightarrow N\left( {a;\,\,3 - a} \right).\)
\(C \in CM:\,\,2x - y - 1 = 0 \Rightarrow C\left( {c;\,\,2c - 1} \right).\)
Vì \(N\) là trung điểm của \(BC \Rightarrow B\left( {2a - c;\,\,7 - 2a - 2c} \right).\)
Theo đề bài ta có \(M\) là trung điểm của \(AB \Rightarrow M\left( {\frac{{2a - c + 2}}{2};\,\,4 - a - c} \right).\)
Lại có \(M \in CM \Rightarrow 2.\frac{{2a - c + 2}}{2} - 4 + a + c - 1 = 0\)
\(\begin{array}{l} \Leftrightarrow 2a - c + 2 - 5 + a + c = 0\\ \Leftrightarrow 3a = 3 \Leftrightarrow a = 1\\ \Rightarrow N\left( {1;\,\,2} \right).\\ \Rightarrow B\left( {2 - c;\,\,5 - 2c} \right).\end{array}\)
Gọi \(P\) là giao điểm của \(CM\) và \(d \Rightarrow \) tọa độ của \(P\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}2x - y - 1 = 0\\x + y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{4}{3}\\y = \frac{5}{3}\end{array} \right. \Rightarrow P\left( {\frac{4}{3};\,\,\frac{5}{3}} \right).\)
Vì \(P \in d \Rightarrow PB = PC\) (tính chất đường trung trực của đoạn thẳng)
\(\begin{array}{l} \Leftrightarrow P{B^2} = P{C^2}\\ \Leftrightarrow {\left( {\frac{4}{3} - 2 + c} \right)^2} + {\left( {\frac{5}{3} - 5 + 2c} \right)^2} = {\left( {\frac{4}{3} - c} \right)^2} + {\left( {\frac{5}{3} - 2c + 1} \right)^2}\\ \Leftrightarrow {\left( {c - \frac{2}{3}} \right)^2} + {\left( {2c - \frac{{10}}{3}} \right)^2} = {\left( {\frac{4}{3} - c} \right)^2} + {\left( {\frac{8}{3} - 2c} \right)^2}\\ \Leftrightarrow 5{c^2} - \frac{{44}}{3}c + \frac{{104}}{9} = 5{c^2} - \frac{{40}}{3}c + \frac{{80}}{9}\\ \Leftrightarrow \frac{4}{3}c = \frac{8}{3} \Leftrightarrow c = 2\\ \Rightarrow C\left( {2;\,\,3} \right).\\ \Rightarrow B\left( {0;\,\,1} \right).\end{array}\)
Chọn A.