Phương pháp giải:

Lời giải chi tiết:

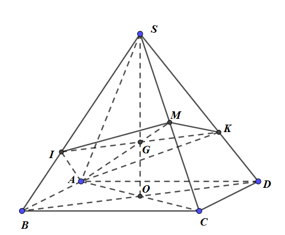
Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên $SO \bot \left( {ABCD} \right)$

Gọi G là giao điểm của AM và SO. Qua G, dựng IK // BD, $\left( {I \in SB,K \in SD} \right)$$\Rightarrow \left( {AIMK} \right) \equiv \left( P \right)$.

Thiết diện của hình chóp $S.ABCD$ cắt bởi $\left( P \right)$ là tứ giác$AIMK$.

Ta có: $\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)$. Mà IK // BD$\Rightarrow IK \bot \left( {SAC} \right) \Rightarrow IK \bot AM \Rightarrow {S_{AIMK}} = \dfrac{1}{2}.IK.AM$

$\Delta SAC$ có $SA = SC = a,\,\,AC = a\sqrt 2  \Rightarrow \Delta SAC$ vuông cân tại S, $AM = \sqrt {S{A^2} + S{M^2}}  = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 5 }}{2}$

G là trọng tâm $\Rightarrow \dfrac{{SG}}{{SO}} = \dfrac{2}{3} \Rightarrow \dfrac{{IK}}{{BD}} = \dfrac{2}{3} \Rightarrow IK = \dfrac{2}{3}.a\sqrt 2  = \dfrac{{2a\sqrt 2 }}{3}$

$\Rightarrow {S_{AIMK}} = \dfrac{1}{2}.\dfrac{{2a\sqrt 2 }}{3}.\dfrac{{a\sqrt 5 }}{2} = \dfrac{{{a^2}\sqrt {10} }}{3}$.

Chọn: B