Phương pháp giải:

Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.

Lời giải chi tiết:

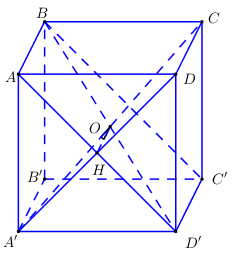
Gọi $O = A'C \cap BD' \Rightarrow O = A'C \cap \left( {ABC'D'} \right)$.

Gọi $H = A'D \cap AD'$ ta có:

$\left\{ \begin{array}{l}AB \bot \left( {ADD'A'} \right) \Rightarrow AB \bot A'H\\A'H \bot AD'\end{array} \right. \Rightarrow A'H \bot \left( {ABC'D'} \right)$

$\Rightarrow HO$ là hình chiếu của $A'O$ trên $\left( {ABC'D'} \right)$

$\Rightarrow \angle \left( {A'C;\left( {ABC'D'} \right)} \right) = \angle \left( {A'O;HO} \right) = \angle A'OH = \alpha$.

Không mất tính tổng quát, ta đặt cạnh của hình lập phương bằng 1.

Xét tam giác vuông $A'OH$ vuông tại $H$ có:

$\left\{ \begin{array}{l}OH = \dfrac{1}{2}AB = \dfrac{1}{2}\\A'H = \dfrac{1}{2}A'D = \dfrac{{\sqrt 2 }}{2}\end{array} \right. \Rightarrow \tan \angle A'OH = \tan \alpha  = \dfrac{{AH}}{{OH}} = \sqrt 2$.

Chọn D