Câu hỏi:
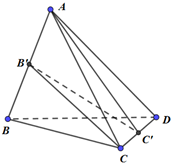
Cho tứ diện \(ABCD\). Gọi \(B',C'\) lần lượt là trung điểm của \(AB\) và \(CD\). Khi đó, tỷ số thể tích của khối đa diện \(AB'C'D\) và khối đa diện \(ABCD\) bằng
- A \(\frac{1}{8}\).
- B \(\frac{1}{6}\).
- C \(\frac{1}{4}\).
- D \(\frac{1}{2}\).
Phương pháp giải:
Lập tỉ số thể tích.
Lời giải chi tiết:
Do B’ là trung điểm của AB nên \({V_{AB'C'D}} = \frac{1}{2}{V_{A.BCC'}}\)
Mà \({V_{ABCC'}} = \frac{1}{2}.{V_{ABCD}}\) (do C’ là trung điểm của CD) \( \Rightarrow \frac{{{V_{AB'C'D}}}}{{{V_{ABCD}}}} = \frac{1}{4}\)
Chọn: C
Quảng cáo
Câu hỏi trước
