Câu hỏi:
Cho khối nón \(\left( N \right)\) có góc ở đỉnh bằng \({90^0}\) và diện tích xung quanh bằng \(4\sqrt 2 \pi \). Thể tích của khối nón đã cho bằng:
- A \(\frac{{8\pi }}{3}\)
- B \(\frac{{4\pi }}{3}\)
- C \(8\pi \)
- D \(4\pi \)
Phương pháp giải:
Diện tích xung quanh hình nón có bán kính đáy \(r\), đường sinh \(l\) là \({S_{xq}} = \pi rl\).
Thể tích khôi nón có bán kính đáy \(r\), chiều cao \(h\) là \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
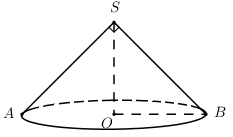
Tam giác \(SAB\) vuông cân tại \(S \Rightarrow \angle SBA = {45^0} \Rightarrow \Delta SOB\) vuông cân tại \(O\).
Đặt \(OB = r \Rightarrow SB = r\sqrt 2 ;\,\,SO = r\).
Khi đó ta có \({S_{xq}} = \pi OB.SB = \pi .r.r\sqrt 2 = 4\sqrt 2 \pi \Leftrightarrow {r^2} = 4 \Leftrightarrow r = 2\).
Vậy thể tích khối nón là: \(V = \frac{1}{3}\pi O{B^2}.SO = \frac{1}{3}\pi {.2^2}.2 = \frac{{8\pi }}{3}\).
Chọn A.