Câu hỏi:
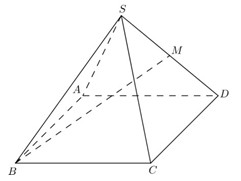
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(SD\) (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng \(BM\) và mặt phẳng \(\left( {ABCD} \right)\) bằng:
- A \(\dfrac{2}{3}.\)
- B \(\dfrac{1}{3}.\)
- C \(\dfrac{{\sqrt 3 }}{2}.\)
- D \(\dfrac{{\sqrt 2 }}{2}.\)
Phương pháp giải:
Góc giữa đường thẳng và mặt phẳng cắt nhau là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Lời giải chi tiết:
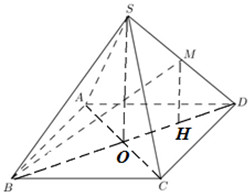
Gọi \(O = AC \cap BD\). Do chóp \(S.ABCD\) đều \( \Rightarrow SO \bot \left( {ABCD} \right)\).
Trong \(\left( {SBD} \right)\) kẻ \(MH//SO\,\,\left( {H \in BD} \right) \Rightarrow MH \bot \left( {ABCD} \right)\).
\( \Rightarrow \angle \left( {BM;\left( {ABCD} \right)} \right) = \angle \left( {BM;BH} \right) = \angle MBH\).
\(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \).
\( \Rightarrow OB = OD = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\).
Dễ thấy \(MH\) là đường trung bình của \(\Delta SOD \Rightarrow H\) là trung điểm của \(OD\) và \(MH = \dfrac{1}{2}SO\).
\( \Rightarrow BH = \dfrac{3}{4}BD = \dfrac{{3a\sqrt 2 }}{4}\) và \(MH = \dfrac{1}{2}SO = \dfrac{1}{2}\sqrt {S{D^2} - O{D^2}} = \dfrac{1}{2}\sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{4}\).
Trong tam giác vuông \(BMH\) có: \(\tan \angle MBH = \dfrac{{MH}}{{BH}} = \dfrac{{\dfrac{{a\sqrt 2 }}{4}}}{{\dfrac{{3a\sqrt 2 }}{4}}} = \dfrac{1}{3}\).
Vậy \(\tan \angle \left( {BM;\left( {ABCD} \right)} \right) = \dfrac{1}{3}\).
Chọn B.


















