Câu 71 trang 128 Sách bài tập Hình học 11 Nâng cao

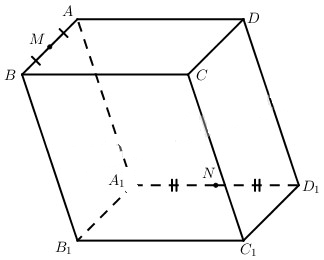
Đề bài

Cho M và N lần lượt là trung điểm của các cạnh AB, A­₁D₁ của hình hộp ABCD.A₁B₁C₁D₁.

a) Xác định giao điểm P và Q của mặt phẳng (CMN) với các đường thẳng B₁C₁ và DB₁.

b) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\overrightarrow {AQ} \) qua các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)  trong đó \(\overrightarrow b  = \overrightarrow {AB} ,\overrightarrow c  = \overrightarrow {A{\rm{D}}} ,\overrightarrow a  = \overrightarrow {A{A_1}} \).

Lời giải chi tiết

a) Đặt \(\overrightarrow {A{A_1}}  = \overrightarrow a ,\overrightarrow {AB}  = \overrightarrow b ,\overrightarrow {AD}  = \overrightarrow c \).

P là giao điểm của mp(CMN) với đường thẳng B₁C₁ khi và chỉ khi C, M, N, P thuộc một mặt phẳng và P thuộc đường thẳng B₁C₁.

Ta có các điểm M, N, C, P thuộc một mặt phẳng nên tồn tại các số x, y, z sao cho:

\(x + y + z = 1\,\,\,\,\,\,\,\,\,\,\,\left( * \right)\)

và \(\overrightarrow {AP}  = x\overrightarrow {AM}  + y\overrightarrow {AN}  + z\overrightarrow {AC.} \)

Ta có:

\(\eqalign{  & \overrightarrow {AP}  = x.{{\overrightarrow b } \over 2} + y\left( {\overrightarrow a  + {{\overrightarrow c } \over 2}} \right) + z\left( {\overrightarrow b  + \overrightarrow c } \right)  \cr  &  = y\overrightarrow a  + \left( {{x \over 2} + z} \right)\overrightarrow b  + \left( {{y \over 2} + z} \right)\overrightarrow c \,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr} \)

Vì P thuộc đường thẳng B₁C₁ nên \(\overrightarrow {{B_1}P}  = t\overrightarrow {{B_1}{C_1}} \), từ đó \(\overrightarrow {AP}  = \overrightarrow b  + \overrightarrow a  +t \overrightarrow c \,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)

Từ (1), (2) và do \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng nên

\(\left\{ \matrix{  y = 1 \hfill \cr  {x \over 2} + z = 1 \hfill \cr  {y \over 2} + z = t \hfill \cr}  \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {**} \right)\)

Kết hợp (*) và (**), ta có:

\(\eqalign{  & \left\{ \matrix{  y = 1 \hfill \cr  {x \over 2} + z = 1 \hfill \cr  {y \over 2} + z = t \hfill \cr  x + y + z = 1 \hfill \cr}  \right.  \cr  &  \Rightarrow z =  - x \Rightarrow {x \over 2} - x = 1 \Leftrightarrow x =  - 2  \cr  &  \Rightarrow z = 2,t = {5 \over 2} \cr} \)

Vậy giao điểm của mp(CMN) với đường thẳng B₁C₁ là điểm P xác định bời

\(\overrightarrow {{B_1}P}  = {5 \over 2}\overrightarrow {{B_1}{C_1}} \) .

Tương tự như trên, nếu gọi Q là giao điểm của mp(CMN) với đường thẳng B₁D thì ta có \(x + y + z = 1\).

và

\(\eqalign{  & \overrightarrow {AQ}  = x\overrightarrow {AM}  + y\overrightarrow {AN}  + z\overrightarrow {AC}   \cr  &  = y\overrightarrow a  + \left( {{x \over 2} + z} \right)\overrightarrow b  + \left( {{y \over 2} + z} \right)\overrightarrow c  \cr} \)

Mặt khác

\(\overrightarrow {AQ}  = \overrightarrow b  + \overrightarrow a  + t\overrightarrow {{B_1}D}\)

\(  = \overrightarrow a  + \overrightarrow b  + t\left( { - \overrightarrow a  - \overrightarrow b  + \overrightarrow c } \right) \)

\(= \left( {1 - t} \right)\overrightarrow a  + \left( {1 - t} \right)\overrightarrow b  + t\overrightarrow c\)

Ta có hệ phương trình sau:

\(\eqalign{  & \left\{ \matrix{  y = 1 - t \hfill \cr  {x \over 2} + z = 1 - t \hfill \cr  {y \over 2} + z = t \hfill \cr  x + y + z = 1 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x \over 2} - y + z = 0 \hfill \cr  x + y + z = 1 \hfill \cr  {x \over 2} + {y \over 2} + 2{\rm{z}} = 1 \hfill \cr}  \right.  \cr  &  \Rightarrow 1 - z = 2 - 4{\rm{z}} \Leftrightarrow z = {1 \over 3}  \cr  &  \Rightarrow x = {2 \over 9},y = {4 \over 9},t = {5 \over 9}. \cr} \)

Vậy giao điểm Q của đường thẳng B₁D với mp(CMN) được xác định bởi

\(\overrightarrow {{B_1}Q}  = {5 \over 9}\overrightarrow {{B_1}D} \)

b) Từ kết quả của câu a), ta có :

\(\eqalign{  & \overrightarrow {AP}  = \overrightarrow a  + \overrightarrow b  + {5 \over 2}\overrightarrow c   \cr  & \overrightarrow {AQ}  = {4 \over 9}\overrightarrow a  + {4 \over 9}\overrightarrow b  + {5 \over 9}\overrightarrow c  \cr} \).

Loigiaihay.com