Bài 7 trang 146 SGK Giải tích 12

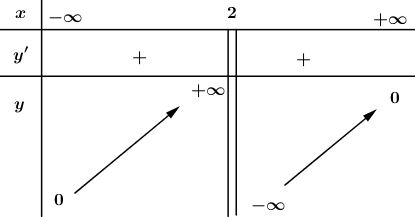
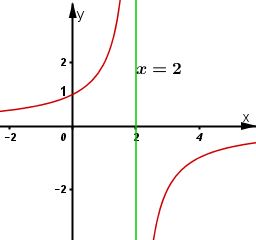
LG a

a) Khảo sát sự biến thiên và vẽ đồ thị $(C)$  của hàm số đã cho.

Phương pháp giải:

Khảo sát và vẽ đồ thị hàm số theo các bước đã được học.

Lời giải chi tiết:

- Tập xác định: $D=(-∞, 2) ∪(2, +∞).$

- Sự biến thiên: $\displaystyle y' = {2 \over {{{(2 - x)}^2}}} > 0,\forall x \in D$

Nên hàm số đồng biến trên hai khoảng này.

- Hàm số không có cực trị

- Giới hạn tại vô cực và tiệm cận ngang

$\displaystyle \mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } {2 \over {2 - x}} = 0;$ $\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } {2 \over {2 - x}} = 0$

$\Rightarrow y = 0$ là tiệm cận ngang của đồ thị hàm số.

- Giới hạn vô cực và tiệm cận đứng:

$\displaystyle \mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} ({2 \over {2 - x}}) =  - \infty ;$ $\displaystyle \mathop {\lim }\limits_{x \to {2^ - }}  = \mathop {\lim }\limits_{x \to {2^ - }} ({2 \over {2 - x}}) =  + \infty$

$\Rightarrow x = 2$ là tiệm cận đứng của đồ thị hàm số.

- Bảng biến thiên:

Đồ thị hàm số:

Đồ thị hàm số:

Đồ thị cắt trục tung tại điểm có tung độ $y = 1$, không cắt trục hoành.

LG b

b) Tìm các giao điểm của $(C)$  và đồ thị của hàm số  $y=x^2+1.$ Viết phương trình tiếp tuyến của $(C)$  tại mỗi giao điểm.

Phương pháp giải:

Giải phương trình hoành độ giao điểm của đồ thị hàm số $(C)$ với đồ thị hàm số $y=x^2+1$ tìm các giao điểm.

+) Sau đó lập phương trình tiếp tuyến của đồ thị hàm số $(C)$ dựa vào công thức: Phương trình tiếp tuyến của đồ thị hàm số $y=f(x)$ tại điểm $x=x_0$ có công thức: $y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.$

Lời giải chi tiết:

Phương trình xác định hoành độ giao điểm của hai đồ thị là:

$\displaystyle {2 \over {2 - x}} = {x^2} + 1$ $\Leftrightarrow {x^3} - 2{x^2} + x = 0 \Leftrightarrow x \in \left\{ {0,1} \right\}$

Hai đồ thị cắt nhau tại hai điểm $M_1(0; \, 1); \, M_2(1; \, 2).$

Tiếp tuyến với đồ thị (C): $\displaystyle y = {2 \over {2 - x}}$ tại điểm $M_1$ có phương trình là:

$y = y'\left( 0 \right)\left( {x - 0} \right) + 1 = \dfrac{1}{2}x + 1$.

Tiếp tuyến  tại điểm $M_2$ có phương trình $y =y'(1)(x-1)+2$ $= 2(x – 1) + 2 = 2x.$

LG c

c) Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng H giới hạn bởi đồ thị (C) và các đường thẳng $y = 0, \,  x = 0,  \, x = 1$ xung quanh trục $Ox.$

Phương pháp giải:

Khi quay hình phẳng được giới hạn bởi các đồ thị hàm số $y=f(x), \, y=g(x)$ và các đường thẳng $x=a, \, \, x=b \, (a<b)$ quanh trục $Ox$ có thể tích được tính bởi công thức:

$$V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx.}$$

Lời giải chi tiết:

Trong khoảng $(0; 1)$ đồ thị (C) nằm phía trên trục hoành nên thể tích cần tính là :

$\displaystyle V = \pi \int_0^1 {({2 \over {2 - x}}} {)^2}dx  = \left. {\pi .\frac{4}{{2 - x}}} \right|_0^1$ $= 2\pi.$

Loigiaihay.com