Câu 3.72 trang 97 sách bài tập Đại số và Giải tích 11 Nâng cao

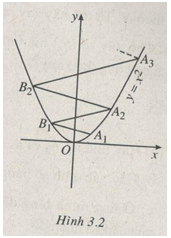
Đề bài

Trong mặt phẳng tọa độ, trên parabol \(y = {x^2}\) lấy dãy các điểm \(({A_n})\) và \(({B_n})\) sao cho điểm \({A_1}\) có hoành độ dương và với mỗi số nguyên dương n, đường thẳng \({A_n}{B_n}\) có hệ số góc bằng \( - {1 \over 5}\) và đường thẳng \({B_n}{A_{n + 1}}\) có hệ số góc bằng \({1 \over 4}.\) (h.3.2).

Với mỗi số nguyên dương n, kí hiệu \({a_n}\) và \({b_n}\) tương ứng với hoành độ của \({A_n}\) và \({B_n}\).

Chứng minh rằng các dãy số \(({a_n})\) và\(({b_n})\) là các cấp số cộng. Hãy xác định công sai và số hạng tổng quát của mỗi cấp số cộng đó.

Lời giải chi tiết

Với mỗi \(n \ge 1,\) do \({A_n}\) và \({B_n}\)  nằm trên parabol \(y = {x^2}\) nên  \({A_n} = \left( {{a_n};a_n^2} \right)\) và \({B_n} = \left( {{b_n};b_n^2} \right)\). Từ đó:

- Do đường thẳng \({A_n}{B_n}\) có hệ số góc bằng \(- {1 \over 5}\) nên \({a_n} + {b_n} =  - {1 \over 5}\) với mọi \(n \ge 1;\)

- Do đường thẳng \({B_n}{A_{n + 1}}\) có hệ số góc bằng \({1 \over 4}\) nên \({a_{n + 1}} + {b_n} = {1 \over 4}\) với mọi \(n \ge 1;\)

Suy ra với mọi \(n \ge 1,\) ta có

\({a_{n + 1}} - {a_n} = {9 \over {20}}\) và \({b_{n + 1}} - {b_n} =  - {9 \over {20}}.\)

Vì thế:

- Dãy số \(({a_n})\) là một cấp số cộng với số hạng đầu \({a_1}\) và công sai \(d = {9 \over {20}};\)

- Dãy số \(({b_n})\) là một cấp số cộng với số hạng đầu \({b_1} =  - {1 \over 5} - {a_1}\) và công sai \(d =  - {9 \over {20}}.\)

Số hạng tổng quát : \({a_n} = {a_1} + \left( {n - 1} \right) \times {9 \over {20}}\) và \({b_n} =  - {1 \over 5} - {a_1} - \left( {n - 1} \right) \times {9 \over {20}}\).

Loigiaihay.com