Câu 34 trang 120 Sách bài tập Hình học 11 Nâng cao

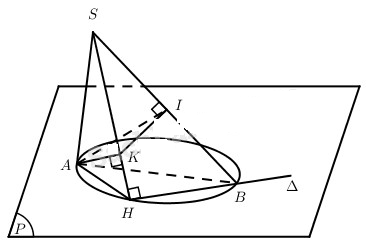
Đề bài

Trong mặt phẳng (P) cho hai điểm A và B phân biệt. Đoạn thẳng SA vuông góc với mặt phẳng (P). Gọi ∆ là đường thẳng nằm trong (P) và đi qua điểm B, H là chân đường vuông góc kẻ từ điểm S đến ∆.

a) Chứng minh rằng điểm H thuộc một đường tròn cố định khi ∆ thay đổi.

b) Gọi AK là đường cao của tam giác SAH; AI là đường cao của tam giác SAB. Chứng minh rằng điểm K thuộc đường tròn cố định khi ∆ thay đổi. Xác định vị trí của đường thẳng ∆ để diện tích tam giác AKI đạt giá trị lớn nhất.

c) Hãy xác định vị trí của đường thẳng ∆ để độ dài SH đạt giá trị lớn nhất hoặc bé nhất.

Lời giải chi tiết

 Vì \(SA \bot \left( P \right),\Delta  \subset \left( P \right),SH \bot \Delta \) nên \(AH \bot HB\) (định lí ba đường vuông góc). Như vậy \(\widehat {AHB} = {90^0}\). Do A, B cố định thuộc (P), H ∈ (P) nên điểm H thuộc đường tròn đường kính AB cố định trong (P).

b) Vì \(HB \bot \left( {SAH} \right)\) nên \(HB \bot AK\), mặt khác \(AK \bot SH\) nên \(AK \bot \left( {SHB} \right)\).

Vậy \(AK \bot SI\). Do giả thiết \(AI \bot AB\), từ đó \(SB \bot \left( {AKI} \right)\)

S, B, A là các điểm cố định nên mp(AKI) cố định và I cố định.

Do \(AK \bot \left( {SHB} \right)\) nên \(AK \bot KI\). Vậy K thuộc đường tròn đường kính AI trong mặt phẳng (AKI) cố định nói trên. Đó chính là đường tròn cố định chứa điểm K.

- Đặt \(\widehat {ABH} = \alpha \) thì

\(AH = AB\sin \alpha  = 2{\rm{R}}\sin \alpha \,\,\,\,\,\,\,\,\,\left( {AB = 2{\rm{R}}} \right)\).

Ta có tam giác AKI vuông tại K với cạnh huyền AI cố định, từ đó diện tích tam giác AKI đạt giá trị lớn nhất khi và chỉ khi AKI là tam giác vuông cân, lúc đó \(AK = {{AI} \over {\sqrt 2 }}\).

Mặt khác \({1 \over {A{K^2}}} = {1 \over {{\rm{A}}{{\rm{S}}^2}}} + {1 \over {A{H^2}}} = {1 \over {{h^2}}} + {1 \over {4{{\rm{R}}^2}{{\sin }^2}\alpha }}\).

hay \({2 \over {A{I^2}}} = {1 \over {{h^2}}} + {1 \over {4{R^2}{{\sin }^2}\alpha }}\,\,\,\,\,\,\,\,\,\,\,\,\left( {h = SA} \right)\) .

Vì AI là đường cao của tam giác vuông SAB nên

 \({1 \over {A{I^2}}} = {1 \over {{h^2}}} + {1 \over {4{R^2}}}.\)

Vậy \({S_{AKI}}\) đạt giá trị lớn nhất khi α thỏa mãn điều kiện

\(\eqalign{  & {2 \over {{h^2}}} + {2 \over {4{{\rm{R}}^2}}} = {1 \over {{h^2}}} + {1 \over {4{{\rm{R}}^2}{{\sin }^2}\alpha }}  \cr  &  \Leftrightarrow {1 \over {{h^2}}} + {2 \over {4{{\rm{R}}^2}}} = {1 \over {4{{\rm{R}}^2}{{\sin }^2}\alpha }}  \cr  &  \Leftrightarrow {{4{R^2} + 2{h^2}} \over {{h^2}}} = {1 \over {{{\sin }^2}\alpha }}  \cr  &  \Leftrightarrow \sin \alpha  = {h \over {\sqrt {4{R^2} + 2{h^2}} }} \cr} \)

Như vậy, có hai vị trí của đường thẳng ∆ để \({S_{AKI}}\) đạt giá trị lớn nhất.

c) Ta có SH lớn nhất khi và chỉ khi AH lớn nhất, điều này xảy ra khi AH trùng AB. Vậy nếu ∆ trong (P) vuông góc với AB tại B thì SH đạt giá trị lớn nhất.

SH đạt giá trị bé nhất khi và chỉ khi AH đạt giá trị bé nhất, điều này xảy ra khi H trùng với điểm A, tức là ∆ trùng với đường thẳng AB.

Loigiaihay.com