Bài 30 trang 10 SBT Hình Học 11 nâng caoGiải bài 30 trang 10 sách bài tập Hình Học 11 nâng cao. Cho hai điểm A, B phân biệt. Chứng minh rằng nếu phép dời hình F biến A thành B và biến B thành A thì F là phép đối xứng trục hoặc phép đối xứng tâm... Quảng cáo
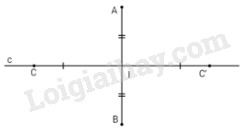
Đề bài Cho hai điểm A, B phân biệt. Chứng minh rằng nếu phép dời hình F biến A thành B và biến B thành A thì F là phép đối xứng trục hoặc phép đối xứng tâm. Lời giải chi tiết Vì F biến A thành B và biến B thành A nên F biến trung điểm I của AB thành chính nó. Nếu gọi c là đường trung trực của AB thì F biến c thành chính nó. Trên c lấy hai điểm C và C’ đối xứng với nhau qua I thì hoặc F biến C thành C hoặc F biến C thành C'. Nếu F biến C thành C thì F biến tam giác ABC thành tam giác BAC. Vậy F chính là phép đối xứng trục \({Đ_C}\). Nếu F biến C thành C’ thì F biến tam giác ABC thành tam giác BAC’. Vậy F chính là phép đối xứng tâm \({Đ_I}.\)
Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
