Bài 16 trang 148 SGK Giải tích 12Trên mặt phẳng tọa độ, hãy tìm tập hợp điểm biểu diễn số phức z thỏa mãn bất đẳng thức: Quảng cáo
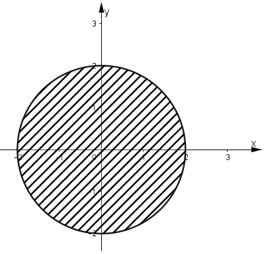
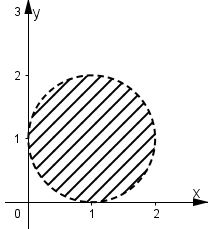
Video hướng dẫn giải Trên mặt phẳng tọa độ, hãy tìm tập hợp điểm biểu diễn số phức \(z\) thỏa mãn bất đẳng thức: LG a a) \(| z| < 2\) Phương pháp giải: Gọi số phức z có dạng \(z = a + bi\), dựa vào các giải thiết đề bài cho thiết lập mối liên hệ giữa a, b và suy ra tập hợp các điểm biểu diễn cho số phức z. Lời giải chi tiết: Đặt \(z = a + bi ( a, b ∈ \mathbb R)\). Ta có: a) \(\left| z \right| < 2 \Leftrightarrow \sqrt {{a^2} + {b^2}} < 2 \) \(\Leftrightarrow {a^2} + {b^2} < 4\) Tập hợp các điểm \(M(a; b)\) là hình tròn tâm \(O\) (gốc tọa độ), bán kính \(2\) (không kể biên)
LG b b) \(|z – i| ≤ 1\) Lời giải chi tiết: \(\eqalign{ Tập hợp các điểm \(M (a; b)\) là hình tròn tâm \(I(0, 1)\), bán kính \(1\) (kể cả biên)
LG c c) \(|z – 1 – i| < 1\) Lời giải chi tiết: \(|z – 1 – i| < 1 ⇔ |(a – 1) + (b – 1)i| < 1 \) \(⇔ (a – 1)^2+ (b – 1)^2 < 1\) Tập hợp các điểm \(M(a; b)\) biểu diễn số phức \(z\) là hình tròn (không kể biên) tâm \(I (1, 1)\), bán kính \(1\).
Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
