Câu 13 trang 52 Sách bài tập Hình học 11 nâng cao.

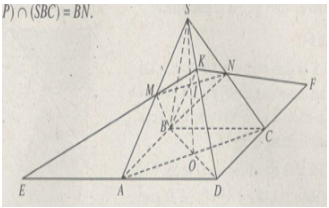
Đề bài

Cho hình chóp S.ABCD có đáy là hình bình hành, O là tâm của đáy; M, N lần lượt là trung điểm của SA, SC. Gọi (P) là mặt phẳng qua M, N và B

a) Tìm giao tuyến của mặt phẳng (P) với các mặt phẳng (SAB), (SBC).

b) Tìm giao điểm I của đường thẳng SO với mp(P) và giao điểm K của đường thẳng SD với mp(P).

c) Xác định giao tuyến của mặt phẳng (P) với mặt phẳng (SAD) và mặt phẳng (SDC).

d) Xác định các giao điểm E, F của các đường thẳng DA, DC với mặt phẳng (P) và chứng tỏ rằng ba điểm E, B, F thẳng hàng.

Lời giải chi tiết

a) \(\eqalign{

& \left( P \right) \cap \left( {SAB} \right) = BM \cr 
& \left( P \right) \cap \left( {SCB} \right) = BN \cr} \)

b) Xét mp(SAC), gọi I là giao điểm của SO và MN thì I là giao điểm của SO và mp(P). Gọi K là giao điểm của đường thẳng BI với SD thì K là giao điểm của SD và (P).

c) \(\left( P \right) \cap \left( {SAD} \right) = MK\)

\(\left( P \right) \cap \left( {SDC} \right) = KN\)

d) Trong mp(SAD) gọi E là giao điểm của đường thẳng MK với đường thẳng AD thì E là giao điểm của (P) và AD.

Tương tự giao điểm F của KN và DC là giao điểm của (P) và DC.

Rõ ràng B, E, F là ba điểm chung của hai mặt phẳng (P) và mp(ABCD) nên chúng phải thẳng hàng.

Loigiaihay.com