Bài 15, 16, 17, 18, 19, 20, 21, 22, 23 trang 19 SBT Hình Học 11 nâng cao

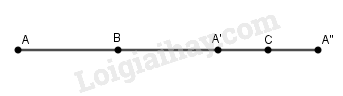
Bài 15

Hợp thành của hai phép đối xứng tâm là phép nào trong các phép sau đây?

(A) Phép đối xứng trục;

(B) Phép đối xứng tâm;

(C) Phép quay;

(D) Phép tịnh tiến.

Lời giải chi tiết:

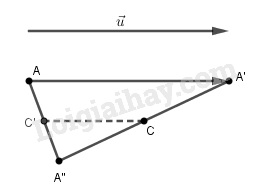
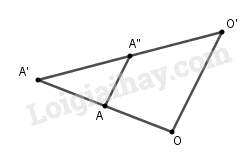
Đáp án: D

Xét hai phép đối xứng tâm B và C ta có:

\(\begin{array}{l}{D_B}\left( A \right) = A' \Rightarrow \overrightarrow {AA'}  = 2\overrightarrow {BA'} \\{D_C}\left( {A'} \right) = A'' \Rightarrow \overrightarrow {A'A''}  = 2\overrightarrow {A'C} \\ \Rightarrow \overrightarrow {AA'}  + \overrightarrow {A'A''}  = 2\overrightarrow {BA'}  + 2\overrightarrow {A'C} \\ \Rightarrow \overrightarrow {AA''}  = 2\left( {\overrightarrow {BA'}  + \overrightarrow {A'C} } \right)\\ \Rightarrow \overrightarrow {AA''}  = 2\overrightarrow {BC} \\ \Rightarrow {T_{\overrightarrow {BC} }}\left( A \right) = A''\end{array}\)

Vậy hợp thành của hai phép đối xứng tâm là phép tịnh tiến.

Bài 16

Hợp thành của một phép tịnh tiến và phép đối xứng tâm là phép nào trong các phép sau đây?

(A) Phép đối xứng trục;

(B) Phép đối xứng tâm;

(C) Phép đồng nhất;

(D) Phép tịnh tiến.

Lời giải chi tiết:

Đáp án: B

Xét phép tịnh tiến theo véc tơ \(\overrightarrow u \) và phép đối xứng qua tâm \(C\) ta có:

\(\begin{array}{l}{T_{\overrightarrow u }}\left( A \right) = A' \Rightarrow \overrightarrow {AA'}  = \overrightarrow u \\{D_C}\left( {A'} \right) = A''\end{array}\)

Gọi \(C'\) là trung điểm của \(AA''\) thì \(\overrightarrow {CC'}  =  - \frac{1}{2}\overrightarrow u \) nên \(C'\) cố định.

Do đó \({D_{C'}}\left( A \right) = A''\).

Vậy hợp thành của phép tịnh tiến và phép đối xứng tâm là một phép đối xứng tâm.

Bài 17

Cho hai đường thẳng song song d và d’. Có bao nhiêu phép vi tự với tỉ số k = 20 biến đường thẳng d thành đường thẳng d’?

(A) Không có phép nào;

(B) Có một phép duy nhất;

(C) Chỉ có hai phép;

(D) Có vô số phép.

Lời giải chi tiết:

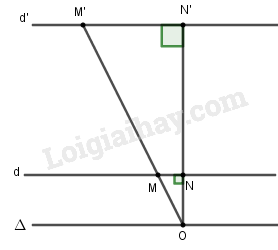
Đáp án: D

Giả sử d và d’ cách nhau một khoảng \(h = NN'\) không đổi.

Gọi O là tâm vị tự thì \({V_{\left( {O;20} \right)}}\left( M \right) = M'\) \( \Leftrightarrow \overrightarrow {OM'}  = 20\overrightarrow {OM} \)

\( \Rightarrow OM' = 20OM\) \( \Rightarrow ON' = 20ON\) \( \Rightarrow NN' = 19ON\) \( \Rightarrow ON = \frac{{NN'}}{{19}} = \frac{h}{{19}}\)

\( \Rightarrow O\) luôn cách \(d\) một khoảng \(\frac{h}{{19}}\) không đổi.

Do đó \(O\) luôn nằm trên đường thẳng \(\Delta \) cách \(d\) một khoảng \(\frac{h}{{19}}\).

Do có vô số điểm \(O\) nên ta có vô số phép vị tự thỏa mãn.

Có vô số phép vị tự thỏa mãn bài toán.

Bài 18

Cho hai đường thẳng cắt nhau d và d’. Có bao nhiêu phép vị tự biến d thành d’?

(A) Không có phép nào;

(B) Có một phép duy nhất;

(C) Chỉ có hai phép;

(D) Có vô số phép.

Lời giải chi tiết:

Đáp án: A

Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó nên không có phép vị tự nào biến đường thẳng d thành d’ mà d và d’ cắt nhau.

Bài 19

Cho hai đường thẳng song song d và d’ và một điểm O không nằm trên chúng. Có bao nhiêu phép vị tự tâm O biến đường thẳng d thành đường thẳng d’?

(A) Không có phép nào;

(B) Có một phép duy nhất;

(C) Chỉ có hai phép;

(D) Có vô số phép.

Lời giải chi tiết:

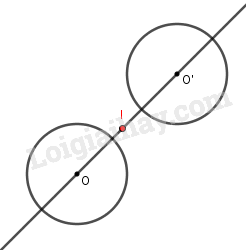
Đáp án: B

Giả sử \(d\left( {O,d} \right) = h,d\left( {O,d'} \right) = h'\).

Xét vị trí điểm \(O\) và hai đường thẳng như hình vẽ.

Khi đó \(\frac{{OM'}}{{OM}} = \frac{{ON'}}{{ON}} = \frac{{h'}}{h}\) \( \Rightarrow \overrightarrow {OM'}  = \frac{{h'}}{h}\overrightarrow {OM} \)

Do đó chỉ có 1 phép vị tự tâm O tỉ số \(k = \frac{{h'}}{h}\) thỏa mãn trong trường hợp này.

Tương tự với trường hợp O nằm trong miền giới hạn bởi d và d’ hay điểm O và d’ cùng nằm trong một mặt phẳng bờ là d thì cũng chỉ có 1 phép vị tự thỏa mãn.

Vậy chỉ có 1 phép vị tự thỏa mãn bài toán.

Bài 20

Cho hai đường tròn bằng nhau (O; R) và (O’; R) với tâm O và O’ phân biệt. Có bao nhiêu phép vị tự biến (O; R) thành (O’; R)?

(A) Không có phép nào;

(B) Có một phép duy nhất;

(C) Chỉ có hai phép;

(D) Có vô số phép.

Lời giải chi tiết:

Đáp án: B

Gọi \(I\) là tâm vị tự và \(k\) là tỉ số vị tự thì:

\({V_{\left( {I;k} \right)}}\left( {\left( {O;R} \right)} \right) = \left( {O';R} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {IO'}  = k\overrightarrow {IO} \\R' = \left| k \right|R\end{array} \right.\)

Ta có: \(R' = \left| k \right|R \Rightarrow k =  \pm 1\)

Nếu \(k = 1\) thì \(\overrightarrow {IO'}  = \overrightarrow {IO}  \Rightarrow O \equiv O'\) (vô lí)

Nếu \(k =  - 1\) thì \(\overrightarrow {IO'}  =  - \overrightarrow {IO} \) hay \(I\) là trung điểm \(OO'\).

Vậy chỉ có 1 phép vị tự duy nhất là \({V_{\left( {I; - 1} \right)}}\).

Bài 21

Cho đường tròn (O; R). Có bao nhiêu phép vị tự với tâm O biến (O; R) thành chính nó?

(A) Không có phép nào;

(B) Có một phép duy nhất;

(C) Chỉ có hai phép;

(D) Có vô số phép.

Lời giải chi tiết:

Đáp án: C

\({V_{\left( {O;k} \right)}}\) biến \(\left( O \right)\) thành chính nó nếu và chỉ nếu \({V_{\left( {O;k} \right)}}\left( O \right) = O\) và \(R = \left| k \right|R \Leftrightarrow k =  \pm 1\)

Vậy chỉ có hai phép vị tự thỏa mãn là \({V_{\left( {O;1} \right)}}\) và \({V_{\left( {O; - 1} \right)}}\).

Bài 22

Cho đường tròn (O;R). Có bao nhiêu phép vị tự biến (O; R) thành chính nó?

(A) Không có phép nào;

(B) Có một phép duy nhất;

(C) Chỉ có hai phép

(D) Có vô số phép.

Lời giải chi tiết:

Đáp án: D

Mọi phép vị tự có tâm bất kì tỉ số \(1\) đều biến đường tròn (O;R) thành chính nó.

Bài 23

Cho hai phép vị tự \({V_{\left( {O;k} \right)}}\) và \({V_{\left( {O';k} \right)}}\) với O và O’ là hai điểm phân biệt và kk’ = 1. Hợp thành của hai phép vị tự đó là phép nào trong các phép sau đây?

(A) Phép tịnh tiến;

(B) Phép đối xứng trục;

(C) Phép đối xứng tâm;

(D) Phép quay.

Lời giải chi tiết:

Đáp án: A

Ta có:

\(\begin{array}{l}{V_{\left( {O;k} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {OA'}  = k\overrightarrow {OA} \\{V_{\left( {O';k'} \right)}}\left( {A'} \right) = A'' \Leftrightarrow \overrightarrow {O'A''}  = k'\overrightarrow {O'A'} \\ \Rightarrow \overrightarrow {OA''}  - \overrightarrow {OO'}  = k'\left( {\overrightarrow {OA'}  - \overrightarrow {OO'} } \right)\\ \Rightarrow \overrightarrow {OA''}  = k'\overrightarrow {OA'}  - k'\overrightarrow {OO'}  + \overrightarrow {OO'} \\ = k'.k\overrightarrow {OA}  - k'\overrightarrow {OO'}  + \overrightarrow {OO'} \\ = \overrightarrow {OA}  + \left( {1 - k'} \right)\overrightarrow {OO'} \\ \Rightarrow \overrightarrow {OA''}  - \overrightarrow {OA}  = \left( {1 - k'} \right)\overrightarrow {OO'} \\ \Rightarrow \overrightarrow {AA''}  = \left( {1 - k'} \right)\overrightarrow {OO'} \\ \Rightarrow {T_{\overrightarrow u }}\left( A \right) = A''\end{array}\)

ở đó \(\overrightarrow u  = \left( {1 - k} \right)\overrightarrow {OO'} \)

Vậy hợp cửa hai phép vị tự trên là phép tịnh tiến theo véc tơ \(\overrightarrow u  = \left( {1 - k} \right)\overrightarrow {OO'} \).

Loigiaihay.com