Bài tập 15 trang 104 Tài liệu dạy – học Toán 8 tập 1

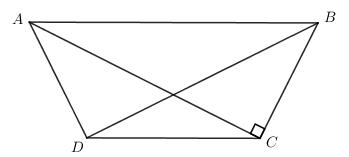
Đề bài

Cho hình thang cân ABCD (CD là đáy bé) có \(\widehat C + \widehat D = 2(\widehat A + \widehat B)\) . Đường chéo AC vuông góc với cạnh bên BC.

a) Tính các góc của hình thang.

b) Chứng minh rằng AC là phân giác của góc \(\widehat {DAB}\).

Lời giải chi tiết

a) Tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\) mà \(\widehat C + \widehat D = 2\left( {\widehat A + \widehat B} \right)\)

Nên \(\widehat A + \widehat B + 2\left( {\widehat A + \widehat B} \right) = {360^0} \Rightarrow 3\left( {\widehat A + \widehat B} \right) = {360^0} \Rightarrow \widehat A + \widehat B = {120^0}\)

Mà \(\widehat A = \widehat B\) (ABCD là hình thang cân)

Nên \(\widehat B + \widehat B = {120^0} \Rightarrow 2\widehat B = {120^0} \Rightarrow \widehat B = {60^0}\).

Vậy \(\widehat A = \widehat B = {60^0}\).

Ta có \(\widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía và AB // CD)

\( \Rightarrow {60^0} + \widehat D = {180^0} \Rightarrow \widehat D = {180^0} - {60^0} = {120^0}\)

Mà \(\widehat C = \widehat D\) (ABCD là hình thang cân). Nên \(\widehat C = \widehat D = {120^0}\)

b) Ta có \(\widehat {BAC} + \widehat B = {90^0}\)  (\(\Delta ACB\) vuông tại C)

\( \Rightarrow \widehat {BAC} + {60^0} = {90^0} \Rightarrow \widehat {BAC} = {30^0}\)

\(\widehat {DAC} = \widehat A - \widehat {BAC} = {60^0} - {30^0} = {30^0}\)

\( \Rightarrow \widehat {DAC} = \widehat {BAC} \Rightarrow AC\) là phân giác của góc DAB.

Loigiaihay.com