Bài 81 trang 129 SGK giải tích 12 nâng caoGiải bất phương trình: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Giải bất phương trình: \(\eqalign{ \(\eqalign{ LG a \({\log _5}\left( {3x - 1} \right) < 1\) Lời giải chi tiết: \(\eqalign{ Vậy \(S = \left( {{1 \over 3};2} \right)\) Cách trình bày khác:
LG b \({\log _{{1 \over 3}}}\left( {5x - 1} \right) > 0\) Lời giải chi tiết: \(\eqalign{ Vậy \(S = \left( {{1 \over 5};{2 \over 5}} \right)\) Cách trình bày khác: ĐK: \(5x - 1 > 0 \Leftrightarrow x > \frac{1}{5}\) BPT \(\begin{array}{l} \Leftrightarrow 5x - 1 < {\left( {\frac{1}{3}} \right)^0} = 1\\ \Leftrightarrow 5x < 2\\ \Leftrightarrow x < \frac{2}{5}\end{array}\) Kết hợp ĐK được \(\frac{1}{5} < x < \frac{2}{5}\) LG c \({\log _{0,5}}\left( {{x^2} - 5x + 6} \right) \ge - 1\) Lời giải chi tiết: \(\eqalign{ Vậy tập nghiệm của bất phương trình là: \(S = \left[ {1;2} \right) \cup \left( {3;4} \right]\) Cách trình bày khác: ĐK:\({x^2} - 5x + 6 > 0 \Leftrightarrow \left[ \begin{array}{l} \(\begin{array}{l} Kết hợp ĐK ta được \(1 \le x < 2\,\,\text { hoặc }\,\,3 < x \le 4\). LG d \({\log _3}{{1 - 2x} \over x} \le 0.\) Lời giải chi tiết: \(\eqalign{ Vậy \(S = \left[ {{1 \over 3};{1 \over 2}} \right)\) Cách trình bày khác: ĐK: \(\frac{{1 - 2x}}{x} > 0 \Leftrightarrow 0 < x < \frac{1}{2}\) Khi đó, \(\begin{array}{l} Kết hợp ĐK ta được \({1 \over 3} \le x < {1 \over 2}\) Loigiaihay.com
|














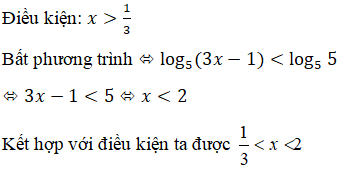






Danh sách bình luận