Bài 8 trang 142 Tài liệu dạy – học Toán 9 tập 2

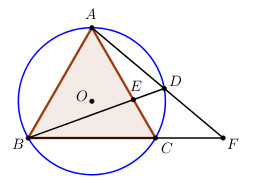
Đề bài

Cho tam giác đều ABC nội tiếp đường tròn tâm O và một điểm D di động trên cung AC. Gọi  E là giao điểm của AC và BD, gọi F là giao điểm của AD và BC. Chứng minh rằng:

a) \(\widehat {AFB} = \widehat {ABD}\)

b) Tích AE.BF không đổi.

Lời giải chi tiết

a) Do tam giác ABC đều \( \Rightarrow AB = AC \Rightarrow \,cung\,AB = cung\,AC\) (hai dây bằng nhau căng hai cung bằng nhau).

Vì \(\widehat {AFB}\) là góc có đỉnh ở bên ngoài đường tròn nên

\(\widehat {AFB} = \dfrac{{sd\,cung\,AB - sd\,cung\,CD}}{2} \)\(\,= \dfrac{{sd\,cung\,AC - sd\,cung\,CD}}{2} \)\(\,= \dfrac{{sd\,cung\,AD}}{2}\).

\(\widehat {ABD}\) là góc nội tiếp đường tròn \(\left( O \right)\) chắn cung AD nên \(\widehat {ABD} = \dfrac{{sd\,cung\,AD}}{2}\).

Vậy \(\widehat {AFB} = \widehat {ABD}\).

b)  Xét tam giác ABD và tam giác AFB có:

\(\widehat {BAF}\) chung;

\(\widehat {ABD} = \widehat {AFB}\,\,\left( {cmt} \right)\)

\( \Rightarrow \Delta ABD \sim \Delta AFB\,\,\left( {g.g} \right)\)

\( \Rightarrow \dfrac{{AB}}{{AF}} = \dfrac{{AD}}{{AB}} = \dfrac{{BD}}{{BF}} \)

\(\Rightarrow BF = \dfrac{{AB.BD}}{{AD}} = \dfrac{{AF.BD}}{{AB}}\)

\( \Rightarrow AE.BF = \dfrac{{AB.BD}}{{AD}}.\dfrac{{BE.AD}}{{BC}}\)\(\, = \dfrac{{AB.BD.AD}}{{BC}} = BD.AD\)

\(\begin{array}{l}\Delta BDF \sim \Delta ADC\end{array}\)

Loigiaihay.com