Bài 12 trang 142 Tài liệu dạy – học Toán 9 tập 2

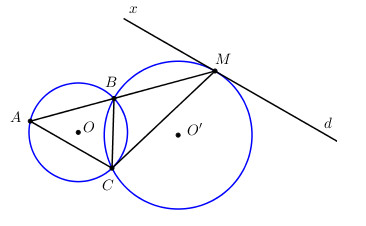
Đề bài

Cho hai đường tròn (O) và (O’) cắt nhau tại B và C. Tiếp tuyến tại C của đường tròn (O) cắt đường tròn (O’) tại điểm thứ hai M. Vẽ cát tuyến MBA (A thuộc đường tròn tâm O). Qua M vẽ tiếp tuyến d của đường tròn (O’). Chứng minh rằng:

a) \(M{C^2} = MA.MB\)

b) AC // d

Lời giải chi tiết

 

a) Xét tam giác MAC và tam giác MCB có:

\(\widehat M\,chung;\)

\(\widehat {MAC} = \widehat {MCB}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC của đường tròn \(\left( O \right)\));

\( \Rightarrow \Delta MAC \sim \Delta MCB\,\,\left( {g.g} \right) \)

\(\Rightarrow \dfrac{{MA}}{{MC}} = \dfrac{{MC}}{{MB}} \Rightarrow M{C^2} = MA.MB\).

b) Ta có: \(\widehat {BMx} = \widehat {MCB}\)  (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC của đường tròn \(\left( {O'} \right)\)).

Mà \(\widehat {MCB} = \widehat {MAC}\) (cmt) \( \Rightarrow \widehat {BMx} = \widehat {MAC}\). Hai góc này ở vị trí so le trong \( \Rightarrow AC//d\,\,\left( {dpcm} \right)\).

 Loigiaihay.com