Bài 17 trang 143 Tài liệu dạy – học Toán 9 tập 2

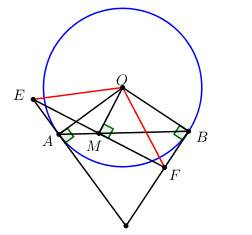
Đề bài

Từ một điểm M trên dây cung AB của đường tròn (O) ta vẽ đường thẳng d vuông góc với OM tại M. Đường thẳng d cắt các tiếp tuyến tại A và B của đường tròn lần lượt tại E và F. Chứng minh M là trung điểm của EF.

Lời giải chi tiết

 

Xét tứ giác OMAE có : \(\widehat {OME} = \widehat {OAE} = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác OMAE là tứ giác nội tiếp (Tứ giác có 2 đỉnh cùng nhìn một cạnh dưới các góc bằng nhau) \( \Rightarrow \widehat {OEM} = \widehat {OAM}\) (1) (hai góc nội tiếp cùng chắn cung OM).

Xét tứ giác OMFB có : \(\widehat {OMF} = \widehat {OBF} = {90^0}\,\,\left( {gt} \right)\) \( \Rightarrow \widehat {OMF} + \widehat {OBF} = {180^0}\) \( \Rightarrow \) Tứ giác OMFB là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰) \( \Rightarrow \widehat {OBM} = \widehat {OFM}\) (2) (hai góc nội tiếp cùng chắn cung OM).

Xét tam giác OAB có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \widehat {OAB} = \widehat {OBA}\) hay \(\widehat {OAM} = \widehat {OBM}\) (3)

Từ (1), (2) và (3) \( \Rightarrow \widehat {OEM} = \widehat {OFM} \Rightarrow \Delta OEF\) cân tại O.

\( \Rightarrow \) Đường cao OM đồng thời là đường trung tuyến.

Vậy M là trung điểm của EF (đpcm).

 Loigiaihay.com