Bài 70 trang 141 SGK Toán 7 tập 1

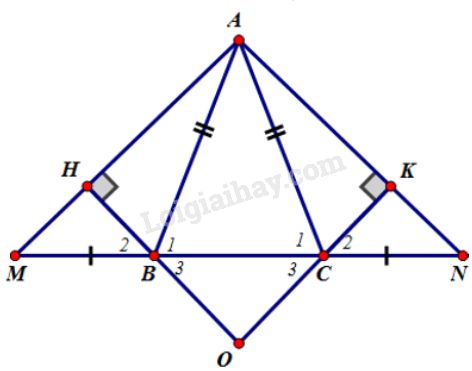
Đề bài

Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của \(BC\) lấy điểm \(M\), trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(BM = CN.\)

a) Chứng minh rằng tam giác \(AMN\) là tam giác cân.

b) Kẻ \(BH ⊥ AM\) (\(H \in AM\)), kẻ \(CK ⊥ AN\; (K  \in  AN).\) Chứng minh rằng \(BH = CK.\)

c) Chứng minh rằng \(AH = AK.\)

d) Gọi \(O\) là giao điểm của \(HB\) và \(KC.\) Tam giác \(OBC\) là tam giác gì? Vì sao?

e) Khi \(\widehat {BAC} = {60^o}\) và \(BM = CN = BC,\) hãy tính số đo các góc của tam giác \(AMN\) và xác định dạng của tam giác \(OBC.\)

Lời giải chi tiết

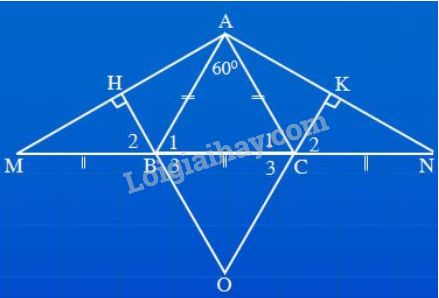
a) \(∆ABC\) cân tại \(A\), suy ra  \(\widehat {{B_1}} = \widehat {{C_1}}\)   (1) 

\(\widehat {{B_1}} + \widehat {ABM} = {180^0}\) (hai góc kề bù)  (2)

\(\widehat {{C_1}} + \widehat {ACN} = {180^0}\) (hai góc kề bù)   (3)

 Từ (1), (2), (3) \(\Rightarrow \widehat {ABM} = \widehat {ACN}\)

Xét \(∆ABM \) và \(∆ACN \) có:

\(AB = AC\) (\(∆ABC\) cân tại \(A\))

\(\widehat {ABM} = \widehat {ACN}\) (chứng minh trên)

\(BM = CN\) (giả thiết)

\( \Rightarrow ∆ABM = ∆ACN\) (c.g.c)

\(\Rightarrow \widehat M = \widehat N\) (hai góc tương ứng)

Vậy \(∆AMN\) là tam giác cân tại \(A.\)

b) Xét hai tam giác vuông \(BHM\) (vuông tại \(H\)) và \(CKN\) (vuông tại \(K\)) có :

\(BM = CN\) (giả thiết)

\(\widehat M = \widehat N\) (chứng minh trên)

\( \Rightarrow ∆BHM  = ∆CKN\) (cạnh huyền - góc nhọn)

\(\Rightarrow BH = CK\) (hai cạnh tương ứng)

c) Theo câu a) ta có tam giác \(AMN\) cân ở \(A\) nên \(AM = AN\) (*)

Theo câu b ta có \(∆BHM = ∆CKN\) nên suy ra \(HM = KN\) (2 cạnh tương ứng) (2*).

Từ (*) và (2*) ta có: \(AH = AM – HM = AN – KN = AK\)

Vậy \(AH = AK.\)

d) \(∆BHM = ∆CKN\) suy ra \(\widehat {{B_2}} = \widehat {{C_2}}\) (hai góc tương ứng)

Mà \(\widehat {{B_2}} = \widehat {{B_3}}\) (2 góc đối đỉnh); \(\widehat {{C_2}} = \widehat {{C_3}}\) (2 góc đối đỉnh)

Nên \(\widehat {{B_3}} = \widehat {{C_3}}\) .

Vậy \(∆OBC\) là tam giác cân tại \(O.\)

e) Khi \(\widehat {BAC} = {60^o}\) và \(BM = CN = BC\) hình được vẽ lại như sau:

+ \(∆ABC\) cân tại \(A\) có \(\widehat {BAC} = {60^o}\) nên là tam giác đều hay \(AB = BC = AC\).

Mặt khác: \(BM = CN = BC\) (giả thiết)

Do đó: \(AB = BC = AC = BM = CN\). 

Vì \(\Delta ABC\) đều nên \(\widehat {B_1} = \widehat {C_1} = {60^o}\)

Ta có \(\widehat {B_1}\) là góc ngoài tại đỉnh \(B\) của tam giác \(ABM\) nên \(\widehat M + \widehat {BAM}=\widehat {B_1}=60^0\) (***)

Vì \(AB = BM\) (chứng minh trên) nên \(∆ABM\) cân tại \(B\) suy ra \(\widehat M = \widehat {BAM}\)

Kết hợp với (***) ta có: \(\widehat M = \widehat {BAM}= \dfrac{60^0}{2}= {30^o}\) .

Lại có \(\Delta AMN\) cân tại \(A\) (câu a)

Suy ra \(\widehat {ANM} = \widehat {AMN} = {30^o}\) .

Theo định lý tổng ba góc trong tam giác \(AMN\) ta có:

\(\widehat {MAN} +{\widehat {AMN} + \widehat {ANM}}= {180^o}  \)

\(\Rightarrow \widehat {MAN} = {180^o} - \left( {\widehat {AMN} + \widehat {ANM}} \right)\)

\( = {180^o} - ({30^o+30^0}) = {120^o}\)

Vậy \(∆AMN\) có \(\widehat M = \widehat N = {30^o};\widehat A = {120^o}.\)

+ \(∆BHM\) vuông tại \(H\) có: \(\widehat M = {30^o}\) nên \(\widehat {{B_2}} =90^0-\widehat M\)\(= 90^0-30^0={60^o}\) (tổng 2 góc nhọn của tam giác vuông bằng \(90^0\))

\(\Rightarrow\) \(\widehat {{B_3}}=\widehat {{B_2}} = {60^o}\) (2 góc đối đỉnh)

\(∆OBC\) cân (theo câu d) có \(\widehat {{B_3}} = {60^o}\) nên \(∆OBC\) đều.