Bài 6 trang 16 Tài liệu dạy – học Toán 9 tập 2Giải bài tập Cho hệ phương trình Quảng cáo
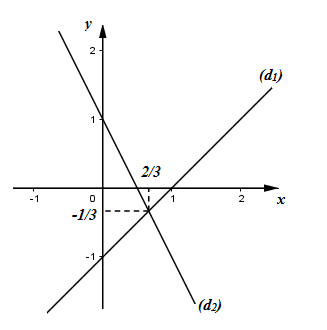
Đề bài Cho hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x + y = 1\end{array} \right.\) Hãy biểu diễn tập nghiệm của mỗi phương trình trong mặt phẳng tọa độ Oxy. Dùng hình vẽ để dự đoán nghiệm của hệ phương trình. Phương pháp giải - Xem chi tiết +) \(ax + by = c \Leftrightarrow y = \dfrac{{ - a}}{b}x + \dfrac{c}{b}\,\,\,\left( d \right)\), do đó tập nghiệm của phương trình \(ax + by = c\) được biểu diễn bởi đường thẳng (d). +) Vẽ các đường thẳng biểu diễn tập nghiệm của mỗi phương trình. +) Xác định giao điểm của hai đường thẳng đó và suy ra nghiệm của hệ phương trình. Lời giải chi tiết \(x - y = 1 \Leftrightarrow y = x - 1\,\,\left( {{d_1}} \right)\) ; \(2x + y = 1 \Leftrightarrow y = - 2x + 1\,\,\left( {{d_2}} \right)\) Ta vẽ hai đường thẳng (d1) và (d2) trên mặt phẳng tọa độ Oxy. Hai đường thẳng (d1) và (d2) cắt nhau tại điểm có tọa độ \(\left( {\dfrac{2}{3}; - \dfrac{1}{3}} \right)\). Vậy hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x + y = 1\end{array} \right.\) có nghiệm \(\left( {x;y} \right) = \left( {\dfrac{2}{3}; - \dfrac{1}{3}} \right)\). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
