Bài 6 trang 40 SGK Hình học 10

Đề bài

Cho hình vuông \(ABCD\). Tính: \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right), \, \sin\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right),\)\(\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right).\)

Lời giải chi tiết

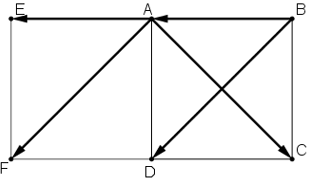
+) Dựng \(\overrightarrow {AE}  = \overrightarrow {BA} \) ta có :

\(\left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) = \left( {\overrightarrow {AC} ,\overrightarrow {AE} } \right) = \widehat {CAE}\)

Mà ABCD là hình vuông nên \(\widehat {BAC} = {45^0}\)

\( \Rightarrow \widehat {CAE} = {180^0} - \widehat {BAC}\) \( = {180^0} - {45^0} = {135^0}\)

\(\begin{array}{l}
\Rightarrow \cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) = \cos {135^0}\\
=  \cos \left( {{{180}^0} - {{45}^0}} \right) = - \cos {45^0}\\
= - \frac{1}{{\sqrt 2 }}
\end{array}\)

Vậy \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) = -\frac{1}{{\sqrt 2 }}\)

+) Dựng \(\overrightarrow {AF}  = \overrightarrow {BD} \) ta có: \(\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {AC} ,\overrightarrow {AF} } \right) = \widehat {CAF}\)

Mà \(\overrightarrow {AF}  = \overrightarrow {BD} \) nên AF//BD.

Lại có AC \(\bot\) BD nên AC \(\bot\) AF hay \(\widehat {CAF}=90^0\).

Vậy \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right) \) \(= \cos \widehat {CAF} = \cos {90^0} = 0\)

+) Vì \(\overrightarrow {AB} ,\overrightarrow {CD} \) là hai véc tơ ngược hướng nên:

\(\left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = {180^0} \) \(\Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \cos {180^0} =  - 1\)

Loigiaihay.com