Bài 5 trang 39 Tài liệu dạy – học Toán 9 tập 2

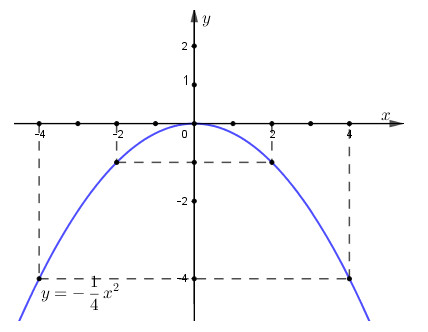
Đề bài

Trên mặt phẳng tọa độ cho parabol (P): \(y = a{x^2}\)

a) Biết (P) đi qua điểm M(2; -1). Tìm hệ số a, vẽ (P) với a vừa tìm được.

b) Tìm tung độ của điểm thuộc parabol có hoành độ x =  - 3.

c) Tìm các điểm thuộc parabol có tung độ y = -9.

Lời giải chi tiết

Trên mặt phẳng tọa độ cho parabol (P): \(y = a{x^2}\)

a) Biết (P) đi qua điểm M(2; -1). Tìm hệ số a, vẽ (P) với a vừa tìm được.

(P) đi qua điểm M(2;-1) nên thay x = 2; y = -1  vào (P) ta được: \( - 1 = a{.2^2} \Leftrightarrow a = \dfrac{{ - 1}}{4}\)

Khi đó (P) cần tìm có dạng: \(y = \dfrac{{ - 1}}{4}{x^2}\)

Bảng giá trị

\(x\)	\( - 4\)	\( - 2\)	0	2	4
\(y =  - \dfrac{1}{4}{x^2}\)	\( - 4\)	\( - 1\)	0	\( - 1\)	\( - 4\)

Vậy đồ thị hàm số \(y =  - \dfrac{1}{4}{x^2}\) là parabol và đi qua các điểm có tọa độ là \(\left( { - 4; - 4} \right);\left( { - 2; - 1} \right);\left( {0;0} \right);\left( {2; - 1} \right);\)\(\,\left( {4; - 4} \right)\)

 

b) Tìm tung độ của điểm thuộc parabol có hoành độ x =  - 3.

Điểm thuộc parabol có hoành độ \(x =  - 3 \Rightarrow y =  - \dfrac{1}{4}.{\left( { - 3} \right)^2} = \dfrac{{ - 9}}{4}\)

Vậy điểm đó có tọa độ là \(\left( { - 3;\dfrac{{ - 9}}{4}} \right)\)

c) Tìm các điểm thuộc parabol có tung độ y = -9.

Điểm thuộc parabol có tung độ y = - 9 nên ta có: \(\dfrac{{ - 1}}{4}{x^2} =  - 9 \Leftrightarrow {x^2} = 36 \Leftrightarrow x =  \pm 6\) .

Khi đó ta có các điểm thuộc parabol có tung độ y = -9 là \(\left( { - 6; - 9} \right);\left( {6; - 9} \right)\)

Loigiaihay.com