Bài 5 trang 145 Tài liệu dạy – học Toán 9 tập 1

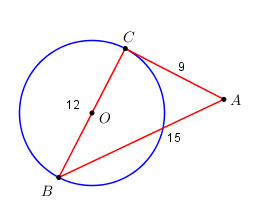
Đề bài

Ở hình dưới, biết AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).

 

Lời giải chi tiết

Ta có :

\(\left\{ \begin{array}{l}A{C^2} + B{C^2} = {9^2} + {12^2} = 225\\A{B^2} = {15^2} = 225\end{array} \right.\)\(\; \Rightarrow A{C^2} + B{C^2} = A{B^2}\).

Do đó theo định lí Pytago đảo ta suy ra \(\Delta ABC\) vuông tại C hay \(AC \bot BC\).

Vì BC là đường kính của \(\left( O \right) \Rightarrow \) AC là tiếp tuyến của \(\left( O \right)\) tại C (dấu hiệu nhận biết tiếp tuyến của đường tròn).

 Loigiaihay.com