Bài 49 trang 135 SGK Đại số 10 nâng caoXét dấu các tam thức bậc hai sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Xét dấu các tam thức bậc hai sau: LG a 3x2 - 2x + 1 Phương pháp giải: Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) Nếu \(\Delta < 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \in \mathbb{R}\) Nếu \(\Delta = 0\) thì f(x) cùng dấu với hệ số a với mọi \(x \ne - \frac{b}{{2a}}\). Nếu \(\Delta > 0\) thì f(x) có hai nghiệm phân biệt \({x_1} < {x_2}\). Khi đó trong khoảng hai nghiệm (\({x_1} < x < {x_2}\)) thì f(x) trái dấu với a, ngoài khoảng hai nghiệm (\(\left[ \begin{array}{l}x > {x_2}\\x < {x_1}\end{array} \right.\)) thì f(x) cùng dấu với a. Lời giải chi tiết: Ta có: a = 3 > 0 Δ’ = 1 – 3 = -2 < 0 ⇒ 3x2 – 2x + 1 > 0,∀x ∈ R LG b -x2 + 4x – 1 Lời giải chi tiết: Ta có: a = -1 < 0 Δ’ = 4 – 1 = 3 > 0 Tam thức -x2 + 4x – 1 có hai nghiệm phân biệt \(x = 2 \pm \sqrt 3 \)
LG c \({x^2} - \sqrt 3 x + {3 \over 4}\) Lời giải chi tiết: Ta có: a = 1 > 0 Δ = 3 – 3 = 0 \({x^2} - \sqrt 3 x + {3 \over 4}\) có nghiệm kép \(x = {{\sqrt 3 } \over 2}\) \( \Rightarrow {x^2} - \sqrt 3 x + {3 \over 4} > 0;\,\forall x \ne {{\sqrt 3 } \over 2}\) LG d \((1 - \sqrt 2 ){x^2} - 2x + 1 + \sqrt 2 \) Lời giải chi tiết: Ta có: \(\eqalign{ Bảng xét dấu:
Loigiaihay.com
|














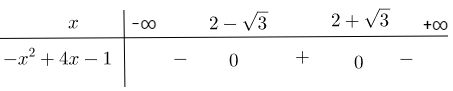







Danh sách bình luận