Bài 49 trang 121 SGK Toán 6 tập 1

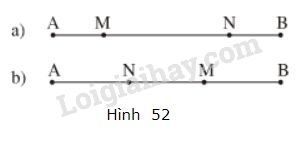
Đề bài

Gọi \(M\) và \(N\) là hai điểm nằm giữa hai mút của đoạn thẳng \(AB\). Biết rằng \(AN=BM\). So sánh \(AM\) và \(BN\). Xét cả hai trường hợp (h.52) 

Lời giải chi tiết

- Vì  \(M\) nằm giữa hai điểm  \(A\) và  \(N\) nên \(AN = AM + MN\)

- Vì  \(N \) nằm giữa hai điểm  \(B\) và  \(M\) nên  \(BM = BN + MN\)

Theo đề bài:  \(AN = BM\) nên  \(AM + MN = BN + MN \Rightarrow  AM = BN\)

(áp dụng tính chất:  \(a + b = c + b \Rightarrow a = c\) ) 

Vậy \(AM = BN\).

- Vì  \(N\) nằm giữa \(A\) và \(M\) nên \(AN + MN= AM\) \(⇒ AN = AM - MN\)

- Vì \(M\) nằm giữa \(B\) và \(N\) nên \(BM + MN= BN\) \(⇒ BM = BN - MN\) 

Theo đề bài: \(AN = BM\) nên \(AM - MN=BN-MN\) \(\Rightarrow AM=BN\) 

(áp dụng tính chất: \(a - b = c - b ⇒ a = c\))

Vậy \(AM = BN\).

Tóm lại: Trong cả hai trường hợp thì hai đoạn thẳng AM và BN có độ dài bằng nhau.

Loigiaihay.com