Đề kiểm tra 15 phút - Đề số 1 - Bài 8, 9 - Chương 1 - Hình học 6Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 8, 9 - Chương 1 - Hình học 6 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
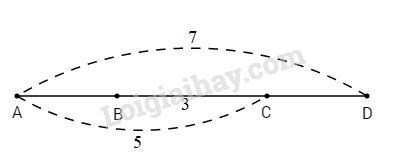
Đề bài Bài 1. Cho điểm B thuộc đoạn thẳng AC, biết AB = 3cm, AC = 7cm. Tính độ dài đoạn thẳng BC. Bài 2. Cho bốn điểm A, B, C, D cùng nằm trên một đường thẳng sao cho B nằm giữa hai điểm A và C, C nằm giữa hai điểm B và D biết rằng: AC = 5cm; BC = 3cm và AD = 7cm. Chứng tỏ rằng: AB = CD. Phương pháp giải: Nếu M nằm giữa hai điểm A và B thì: AM+MB=AB Nếu M nằm giữa hai điểm A và B thì MA và MB là hai tia đối nhau Nếu M nằm giữa hai điểm A và B thì AM và AB là hai tia trùng nhau LG bài 1 Lời giải chi tiết:
Vì B nằm giữa hai điểm A và C nên: \(AB + BC = AC\) \(3 + BC = 7\) \(BC = 7 - 3 = 4\) (cm) LG bài 2 Lời giải chi tiết:
Vì B nằm giữa hai điểm A và C Ta có: \(AB + BC = AC\) \(AB + 3 = 5\) \(AB = 5 - 3 = 2\) (cm) Và khi đó BA và BC là hai tia đối nhau (1) Mặt khác vì C nằm giữa hai điểm B và D nên BC và BD là hai tia trùng nhau (2) Từ (1) và (2) ⇒ BA và BD là hai tia đối nhau nên B nằm giữa hai điểm A và D ta có: \(AB + BD = AD\) \(2 + BD = 7\) \(BD = 7 - 2 = 5\) Lại có C nằm giữa hai điểm B và D \(BC + CD =BD\) \(3 + CD = 5\) \(CD = 5 - 3 = 2\) (cm) Vậy \(AB = CD = 2\) (cm) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
