Bài 47 trang 127 SGK Toán 7 tập 1

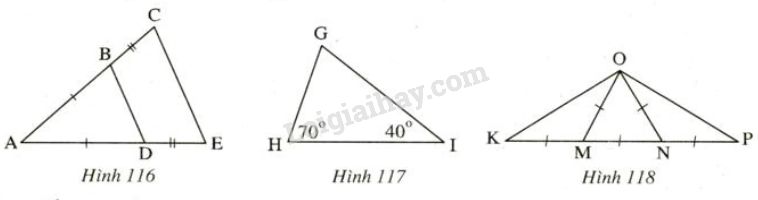
Đề bài

Trong các hình \(116, 117, 118\) tam giác nào là tam giác cân, tam giác nào là tam giác đều? Vì sao?

Lời giải chi tiết

Hình 116

Ta có: \(∆ABD\) cân tại \(A\) vì có \(AB=AD.\)

\(∆ACE\) cân tại \(A\) vì \(AC=AE\) (do \(AB=AD,BC=DE\) nên \(AB+BC=AD+DE\) hay \(AC= AE\)).

Hình 117

Xét tam giác \(GHI\) ta có: \(\widehat{G}+\widehat{H}+ \widehat{I}= {180^o}\) (định lý tổng ba góc trong tam giác)

\(\Rightarrow \widehat{G} = {180^o}- (\widehat{H}+ \widehat{I})\)\(\, = {180^0} - ({70^0} + {40^0}) = {70^0}\)

 Do đó \(∆GHI\) cân tại \(I\) vì \(\widehat{G} = \widehat{H}= {70^0}\)

Hình 118

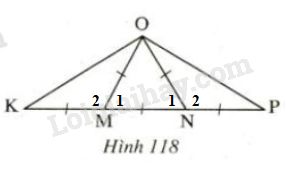
\(∆OMK\) là tam giác cân tại \(M\) vì \(OM= MK\)

\(∆ONP\) là tam giác cân tại \(N\) vì \(ON=NP\)

\(∆OMN\) là tam giác đều vì \(OM = MN = ON\) 

Do đó: \(\widehat {{M_1}} = \widehat {{N_1}} = {60^0}\)   (1)

\(\widehat {{M_1}} + \widehat {{M_2}} = {180^0}\) (hai góc kề bù)    (2)

\(\widehat {{N_1}} + \widehat {{N_2}} = {180^0}\) (hai góc kề bù)     (3)

Từ (1), (2) và (3) suy ra: \(\widehat {{M_2}} = \widehat {{N_2}}\)

Xét \(∆OMK\) và \(∆ONP\) có:

+) \(OM = ON\) (giả thiết)

+) \(\widehat {{M_2}} = \widehat {{N_2}}\) (chứng minh trên)

+) \(MK = NP\) (giả thiết) 

\(\Rightarrow ∆OMK = ∆ONP\) (c.g.c)

\(\Rightarrow \widehat {MKO} = \widehat {NPO}\) (hai góc tương ứng)

Vậy \(∆OKP\) là tam giác cân tại \(O.\) 

Loigiaihay.com