Bài 44 trang 214 SGK Đại số 10 Nâng caoĐơn giản các biểu thức sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đơn giản các biểu thức sau: LG a \(\sin ({\pi \over 3} + \alpha ) - \sin ({\pi \over 3} - \alpha )\) Phương pháp giải: Sử dụng công thức \(\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\) Lời giải chi tiết: Ta có: \(\sin ({\pi \over 3} + \alpha ) - \sin ({\pi \over 3} - \alpha ) \) \(= 2\cos \left( {\frac{{\frac{\pi }{3} + \alpha + \frac{\pi }{3} - \alpha }}{2}} \right)\sin \left( {\frac{{\frac{\pi }{3} + \alpha - \frac{\pi }{3} + \alpha }}{2}} \right)\) \(= 2\cos {\pi \over 3}\sin \alpha = \sin \alpha \) Cách khác: LG b \({\cos ^2}({\pi \over 4} + \alpha ) - {\cos ^2}({\pi \over 4} - \alpha )\) Phương pháp giải: Sử dụng công thức hạ bậc \({\cos ^2}\alpha = \frac{{1 + \cos 2\alpha }}{2}\) Sử dụng công thức: \(\begin{array}{l} Lời giải chi tiết: Áp dụng: \({\cos ^2}a = {{1 + \cos 2a} \over 2}\) , ta có: \(\eqalign{ \(\begin{array}{l} Cách khác: Loigiaihay.com
|














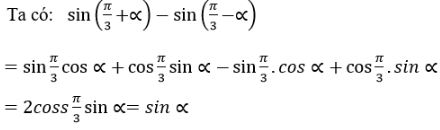
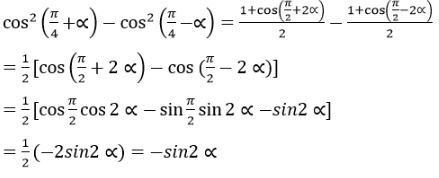






Danh sách bình luận