Bài 4 trang 40 SGK Hình học 10

Đề bài

Chứng minh rằng với mọi góc \(α \, (0^0≤ α ≤ 180^0)\) ta đều có \(\sin ^2\alpha  + {\cos ^2}\alpha  = 1.\)

Lời giải chi tiết

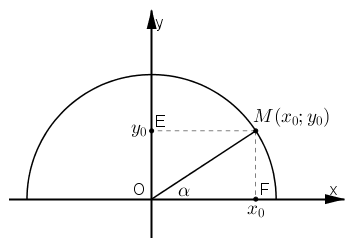
Vẽ nửa đường tròn đơn vị tâm O, bán kính 1 : (O; 1).

Lấy góc α bất kì (0º ≤ α ≤ 180º), luôn  tồn tại điểm M(x₀; y₀) thuộc nửa đường tròn sao cho \(\widehat {xOM} = \alpha \)

Khi đó ta có: \(\sin \alpha  = \frac{{MF}}{{OM}}= MF\) \(\cos \alpha  = \frac{{OF}}{{OM}} = OF\); .

(\(OM = 1\) do \(M \in O\;(0,1)\)).

Ta có:

\({{{\sin }^2}\alpha  + {{\cos }^2}\alpha  = M{F^2} + O{F^2} = O{M^2} = {1^2} = 1}\)

\({ \Rightarrow {{\sin }^2}\alpha  + {{\cos }^2}\alpha  = 1}\)

 

Loigiaihay.com