Bài 36 trang 79 SGK Toán 8 tập 2Tính độ dài x của đường thẳng BD trong hình 43(Làm tròn đến chữ thập phân thứ nhất), biết rằng ABCD là hinh thang(AD // CD); AB= 12,5cm; CD= 28,5cm Quảng cáo
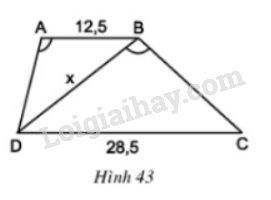
Đề bài Tính độ dài \(x\) của đoạn thẳng \(BD\) trong hình 43 (Làm tròn đến chữ thập phân thứ nhất), biết rằng \(ABCD\) là hình thang (\(AB // CD\)); \(AB= 12,5cm; CD= 28,5cm\); \(\widehat{DAB} = \widehat{DBC}\).
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: - Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. - Tính chất hai tam giác đồng dạng. Lời giải chi tiết Xét \(∆ABD\) và \(∆BDC\) có: +) \(\widehat{DAB}\) = \(\widehat{DBC}\) (giả thiết) +) \(\widehat{ABD}\) = \(\widehat{BDC}\) (AB//CD, hai góc so le trong) \( \Rightarrow ∆ABD ∽ ∆BDC\) (g-g) \( \Rightarrow \dfrac{AB}{BD} = \dfrac{BD}{DC}\) (tính chất hai tam giác đồng dạng) \( \Rightarrow B{D^2} = AB.DC\) \( \Rightarrow BD = \sqrt {AB.DC} = \sqrt {12,5.28,5} \) \( \approx 18,9 cm\)
|




















Danh sách bình luận