Bài 34 trang 17 SGK Toán 8 tập 1Rút gọn các biểu thực sau: Quảng cáo
Video hướng dẫn giải Rút gọn các biểu thức sau: LG a \(\;{\left( {a + b} \right)^2} - {\left( {a - b} \right)^2}\); Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng. \(1)\,{\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\) \(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) \(3)\,{A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) Lời giải chi tiết: \(\eqalign{ Cách 2: \(\eqalign{ LG b \(\,\,{\left( {a + b} \right)^3} - {\left( {a - b} \right)^3} - 2{b^{3}}\) Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng. \(4)\,{\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\) \(5)\,{\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\) \(7)\,{A^3} - {B^3} = \left( {A - B} \right)({A^2} + AB + {B^2})\) Lời giải chi tiết:
LG c \(\;{\left( {x + y + z} \right)^2} - 2\left( {x + y + z} \right)\left( {x + y} \right) + {\left( {x + y} \right)^2}\) Phương pháp giải: Áp dụng các hằng đẳng thức đáng nhớ để khai triển phá ngoặc, sau đó rút gọn các đơn thức đồng dạng. \(2)\,{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) Hoặc áp dụng kết quả: \({\left( {x + y + z} \right)^2} = {x^2} + {y^2} + {z^2} + 2xy + 2yz + 2xz\) Lời giải chi tiết: Đặt \(A=x+y+z; B=x+y\) Ta có: \(\eqalign{ Cách 2:
Loigiaihay.com
|














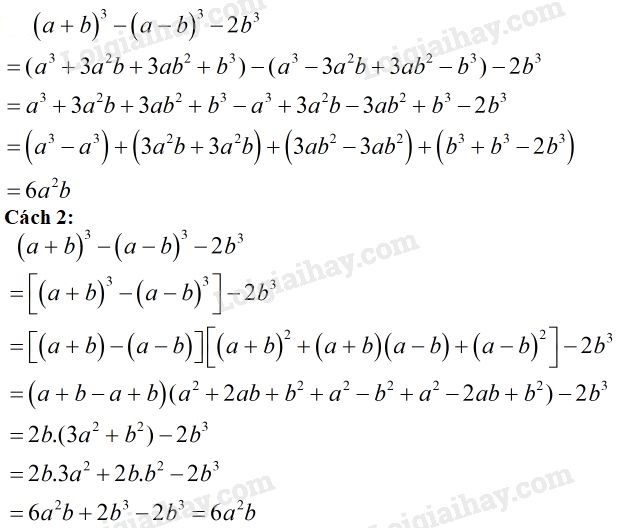
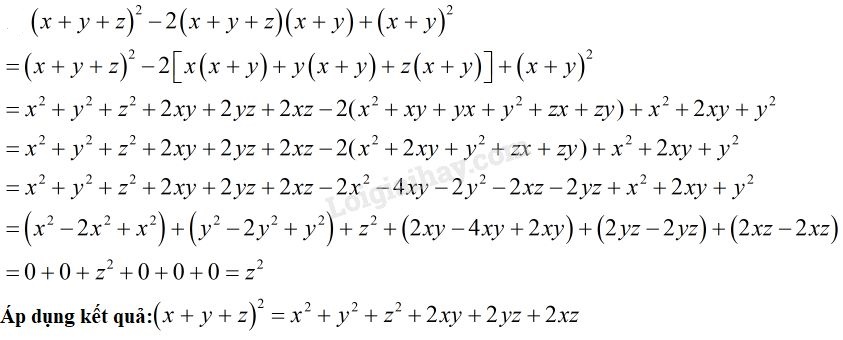






Danh sách bình luận