Bài 3 trang 31 SKG Hình học 12 Nâng caoCho khôi tứ diện ABCD, E và F lần lượt là trung điểm của hai cạnh AB và CD. Hai mặt phẳng (ABF) và (CDE) chia khối tứ diện ABCD thành bốn khối tứ diện. a) Kể tên bốn khối tứ diện đó. b) Chứng tỏ rằng bốn khôi tứ diện đó có thể tích bằng nhau. c) Chứng tỏ rằng nếu ABCD là khối tứ diện đều thì bốn khối tứ diện nói trên bằng nhau. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
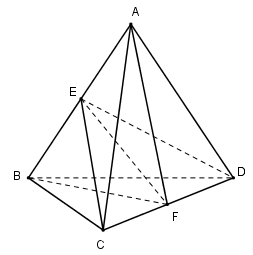
Cho khối tứ diện \(ABCD, E\) và \(F\) lần lượt là trung điểm của hai cạnh \(AB\) và \(CD\). Hai mặt phẳng \((ABF)\) và \((CDE)\) chia khối tứ diện \(ABCD\) thành bốn khối tứ diện. LG a Kể tên bốn khối tứ diện đó. Lời giải chi tiết:
Hai mặt phẳng \((ABF)\) và \((CDE)\) chia khối tứ diện \(ABCD\) thành bốn khối tứ diện \(ADEF, ACEF, BDEF, BCEF\) LG b Chứng tỏ rằng bốn khối tứ diện đó có thể tích bằng nhau. Lời giải chi tiết: Do E là trung điểm của AB nên S∆BEF=S∆AEF ⇒ VCBEF = VCAEF và VDBEF = VDAEF (1) Tương tự S∆CEF = S∆DEF và VACEF = VADEF (2) Từ (1) và (2), suy ra: VBCEF=VADEF=VBDEF=VADEF LG c Chứng tỏ rằng nếu \(ABCD\) là khối tứ diện đều thì bốn khối tứ diện nói trên bằng nhau. Lời giải chi tiết: Nếu \(ABCD\) là tứ diện đều thì nó nhận mp \((ABF)\) và mp \((CDE)\) làm các mặt phẳng đối xứng và phép đối xứng qua đường thẳng \(EF\) biến tứ diện \(ADEF\) thành tứ diện \(BCEF\). Từ đó suy ra: Khối tứ diện \(ADEF\) bằng khối tứ diện \(ACEF\) (vì chúng đối xứng với nhau qua mp \((ABF)\)) Khối tứ diện \(ADEF\) bằng khối tứ diện \(BDEF\) (vì chúng đối xứng với nhau qua mp \((CDE)\)) Khối tứ diện \(ADEF\) bằng khối tứ diện \(BCEF\) (vì phép đối xứng qua trục \(EF\) biến tứ diện này thành tứ diện kia) Cách khác: Ta có: Phép đối xứng qua (ABF) biến: + tứ diện ACEF thành tứ diện ADEF + tứ diện BCEF thành BDEF Phép đối xứng qua (CED) biến: + tứ diện BDEF thành tứ diện ADEF + tứ diện BCEF thành ACEF. Suy ra các tứ diện BCEF, ACEF, ADEF, BDEF bằng nhau. Loigiaihay.com
|




















Danh sách bình luận