Bài 21 trang 60 SGK Hình học 12 Nâng caoCho tam giác ABC vuông tại A, AB = c, AB = b. Tính thể tích của khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi quay quanh đường thẳng BC. Quảng cáo
Đề bài Cho tam giác \(ABC\) vuông tại \(A, AB = c, AB = b\). Tính thể tích của khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi quay quanh đường thẳng \(BC\). Lời giải chi tiết
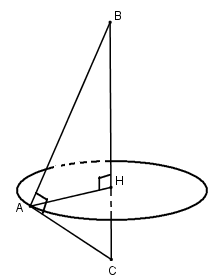
Gọi \(AH\) là đường cao của tam giác \(ABC\). Ta có: \({1 \over {A{H^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}} \) \(\Rightarrow A{H^2} = {{{b^2}{c^2}} \over {{b^2} + {c^2}}}\) Hai tam giác \(ABH\) và \(ACH\) khi quay quanh \(BC\) lần lượt tạo thành hai khối nón \({H_1},{H_2}\) có thể tích lần lượt là \({V_1} = {1 \over 3}\pi A{H^2}BH\,\,,\,\,{V_2} = {1 \over 3}\pi A{H^2}CH\) Thể tích của khối tròn xoay sinh bởi tam giác \(ABC\) khi quay quanh \(BC\) là: \(\eqalign{ Loigiaihay.com
|




















Danh sách bình luận