Bài 10 trang 75 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Cho tam giác ABC vuông cân tại A. Điểm D di động trên cạnh AC. Đường thẳng d vuông góc với AC tại C cắt đường BD tại E. Chứng minh rằng khi D di chuyển trên cạnh AC thì tổng \(\dfrac{1}{{B{D^2}}} + \dfrac{1}{{B{E^2}}}\) không đổi.

Lời giải chi tiết

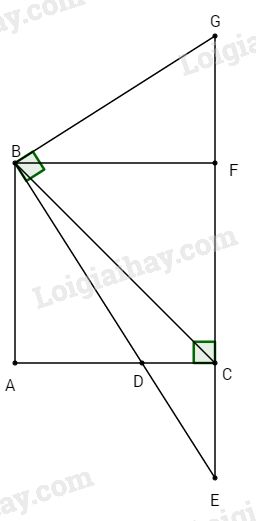
Dựng hình vuông ABFC, qua B kẻ đường thẳng vuông góc với BE cắt đường thẳng CF tại G.

Xét tam giác BFG và tam giác BAD có:

BF = BA (ABFC là hình vuông); \(\widehat {FBG} = \widehat {ABD}\) (cùng phụ với \(\widehat {DBF}\)); \(\widehat {BFG} = \widehat {BAD} = {90^o}\)

\( \Rightarrow \Delta BFG = \Delta BAD\) (g.c.g)

\( \Rightarrow BG = BD\) (2 cạnh tương ứng)

Áp dụng hệ thức lượng trong tam giác BEG vuông tại B, đường cao BF ta có:

\(\dfrac{1}{{B{D^2}}} + \dfrac{1}{{B{E^2}}} = \dfrac{1}{{B{G^2}}} + \dfrac{1}{{B{E^2}}} \)\(\;= \dfrac{1}{{B{F^2}}} = \dfrac{1}{{A{C^2}}}\)không đổi.

Loigiaihay.com