Bài 1 trang 66 SGK Toán 8 tập 1

Đề bài

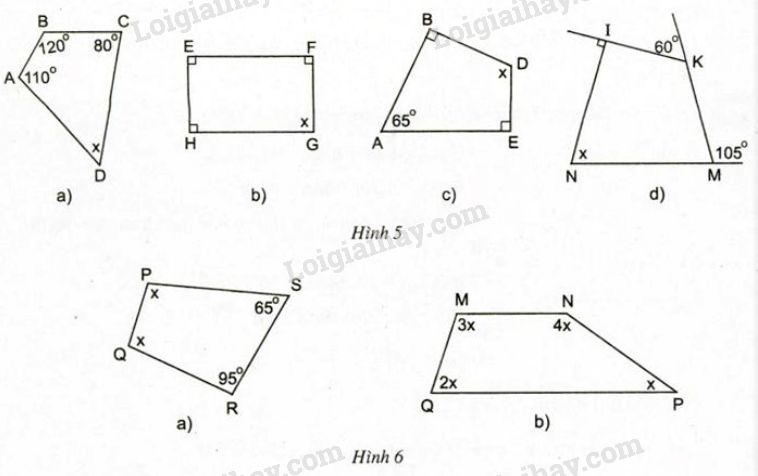
Tìm x ở hình 5, hình 6:

Lời giải chi tiết

Áp dụng: Tổng bốn góc trong 1 tứ giác bằng 360⁰

Ta có:

Ở hình 5

a) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(ABCD\) ta được:

\(\eqalign{
& \,\,\widehat A + \widehat B + \widehat C + \widehat D = {360^0} \cr
& \Rightarrow \widehat D = {360^0} - \left( {\,\,\widehat A + \widehat B + \widehat C} \right) \cr
& \Rightarrow x = {360^0} - \left( {{{110}^0} + {{120}^0} + {{80}^0}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {310^0} = {50^0} \cr} \)

b) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(EFGH\) ta được:

\(\eqalign{
& \widehat E + \widehat F + \widehat G + \widehat H = {360^0} \cr
& \Rightarrow \widehat G = {360^0} - \left( {\widehat E + \widehat F + \widehat H} \right) \cr
& \Rightarrow x = {360^0} - \left( {{{90}^0} + {{90}^0} + {{90}^0}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {270^0} = {90^0} \cr} \)

c) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(ABDE\) ta được:

\(\eqalign{
& \widehat A + \widehat B + \widehat D + \widehat E = {360^0} \cr
& \Rightarrow \widehat D = {360^0} - \left( {\widehat A + \widehat B + \widehat E} \right) \cr
& \Rightarrow x = {360^0} - \left( {{{65}^0} + {{90}^0} + {{90}^0}} \right) \cr
& \;\,\,\,\,\,\,\,\,\,\, = {360^0} - {245^0} = {115^0} \cr} \)

d) Ta có: \(\widehat {IKM}+60^0=180^0\) (hai góc kề bù) \(\Rightarrow \widehat {IKM} = {180^0} - {60^0} = {120^0} \)

\(\widehat {KMN}+105^0=180^0\) (hai góc kề bù) \(\Rightarrow \widehat {KMN} = {180^0} - {105^0} = {75^0}\)

Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(MNIK\) ta được:

\(\eqalign{
& \widehat {KMN} + \widehat {MNI} + \widehat {NIK} + \widehat {IKM} = {360^0} \cr
& \Rightarrow \widehat {MNI} = {360^0} - \left( {\widehat {KMN} + \widehat {IKM} + \widehat {NIK}} \right) \cr
& \Rightarrow x = {360^0} - \left( {{{75}^0} + {{120}^0} + {{90}^0}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {285^0} = {75^0} \cr} \)

Ở hình 6

a) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(PQRS\) ta được:

\(\eqalign{
& \widehat P + \widehat Q + \widehat R + \widehat S = {360^0} \cr
& \Rightarrow \widehat P + \widehat Q = {360^0} - \left( {\widehat S + \widehat R} \right) \cr
& \Rightarrow x + x = {360^0} - \left( {{{65}^0} + {{95}^0}} \right) \cr
& \Rightarrow 2x = {360^0} - {160^0} \cr
& \Rightarrow x = {{{{360}^0} - {{160}^0}} \over 2} \cr
& \Rightarrow x = {{{{200}^0}} \over 2} \cr
& \Rightarrow x = {100^0} \cr} \)

b) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác \(MNPQ\) ta được:

\(\eqalign{
& \widehat M + \widehat N + \widehat P + \widehat Q = {360^0} \cr
& 3x + 4x + x + 2x = {360^0} \cr
& 10x = {360^0} \cr
& x = {{{{360}^0}} \over {10}} = {36^0} \cr} \)

Loigiaihay.com