Bài 1 trang 145 SGK Giải tích 12

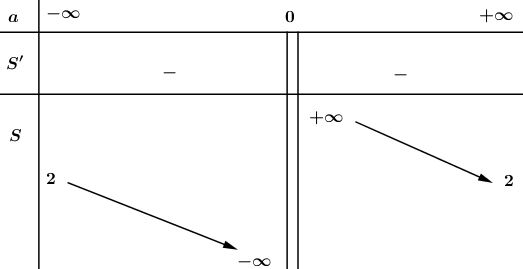
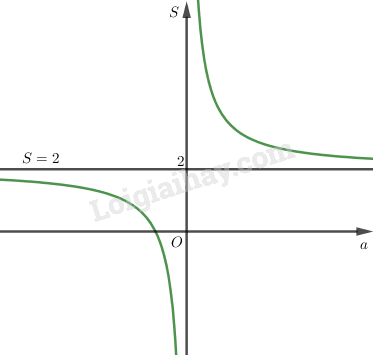
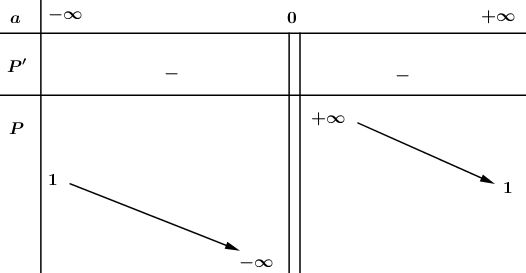
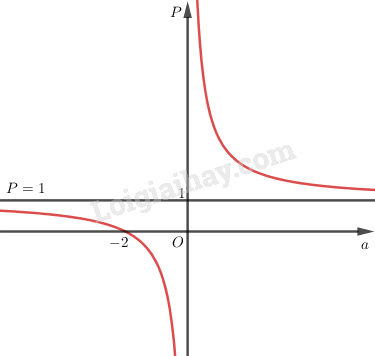
LG a

a) Chứng tỏ rằng phương trình $f(x)  = 0$ luôn có nghiệm thực. Tính các nghiệm đó.

Phương pháp giải:

Nhẩm nghiệm, đưa phương trình $f(x)=0$ về dạng phương trình tích để tìm nghiệm của phương trình.

Lời giải chi tiết:

Ta có:

$f\left( x \right) = 0$ $\Leftrightarrow a{x^2} - 2(a + 1)x + a + 2 = 0$

Phương trình trên có $A = a;B =  - 2\left( {a + 1} \right),C = a + 2$ và

$A + B + C$ $= a - 2\left( {a + 1} \right) + a + 2$ $= a - 2a - 2 + a + 2 = 0$

Do đó phương trình có hai nghiệm phân biệt ${x_1} = 1,{x_2} = \dfrac{C}{A} = \dfrac{{a + 2}}{a}$.

LG b

b) Tính tổng $S$ và tích $P$ của các nghiệm của phương trình $f(x) = 0$. Khảo sát sự biến thiên và vẽ đồ thị hàm số của $S$ và $P$ theo $a$.

Phương pháp giải:

+) Dựa vào hệ thức Vi-ét để tính tổng và tích các nghiệm của phương trình $f(x)=0.$

+) Khảo sát sự biến thiên của đồ thị hàm số và vẽ đồ thị hàm số qua các bước đã được học.  

Lời giải chi tiết:

* Theo định lí Vi-et, tổng và tích của các nghiệm đó là:

$\displaystyle S = {{2a + 2} \over a},P = {{a + 2} \over a}$

* Khảo sát sự biến thiên và vẽ đồ thị hàm số $\displaystyle S = {{2a + 2} \over a} = 2 + {2 \over a}$

- Tập xác định : $(-∞; 0) ∪ (0,\; +∞)$

- Sự biến thiên: $\displaystyle S' =  - {2 \over {{a^2}}} < 0,\forall a \in ( - \infty ; 0) \cup (0; + \infty )$ nên hàm số nghịch biến trên hai khoảng $(-∞; 0)$ và $(0; +∞)$

- Cực trị: Hàm số không có cực trị.

- Giới hạn tại vô cực và tiệm cận ngang.

$\eqalign{ & \mathop {\lim }\limits_{a \to + \infty } S = \mathop {\lim }\limits_{a \to + \infty } (2 + {2 \over a}) = 2 \cr  & \mathop {\lim }\limits_{a \to - \infty } S = \mathop {\lim }\limits_{a \to - \infty } (2 + {2 \over a}) = 2 \cr}$

Vậy $S = 2$ là tiệm cận ngang

- Giới hạn vô cực và tiệm cận đứng:

$\eqalign{ & \mathop {\lim }\limits_{a \to {0^ + }} S = \mathop {\lim }\limits_{a \to {0^ + }} (2 + {2 \over a}) = + \infty \cr  & \mathop {\lim }\limits_{a \to {0^ - }} S = \mathop {\lim }\limits_{a \to {0^ - }} (2 + {2 \over a}) = - \infty \cr}$

Vậy $a = 0$ là tiệm cận đứng.

- Bảng biến thiên:

Đồ thị hàm số:

Đồ thị không cắt trục tung, cắt trục hoành tại $a = -1$

* Khảo sát sự biến thiên và vẽ đồ thị hàm số $\displaystyle P = {{a + 2} \over a} = 1 + {2 \over a}$

Tập xác định: $D = \mathbb R\backslash {\rm{\{ }}0\}$

 $\displaystyle P' = {{ - 2} \over {{a^2}}} < 0,\forall a \in D$

$\mathop {\lim }\limits_{a \to {0^ - }} S =  - \infty  ⇒$ Tiệm cận đứng: $a = 0$

$\mathop {\lim }\limits_{a \to  \pm \infty } S = 1⇒$ Tiệm cận ngang: $P = 1$

Đồ thị hàm số:

Ngoài ra: đồ thị hàm số $\displaystyle P = {{a + 2} \over a} = 1 + {2 \over a}$ có thể nhận được bằng cách tịnh tiến đồ thị $\displaystyle S = {{2a + 2} \over a} = 2 + {2 \over a}$ dọc theo trục tung xuống phía dưới $1$ đơn vị.

Loigiaihay.com