Trả lời câu hỏi 2 Bài 2 trang 84 SGK Toán 7 Tập 1

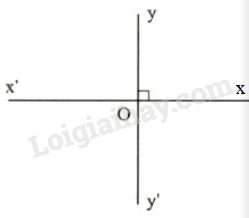
Đề bài

Tập suy luận

Ở hình \(4\), hai đường thẳng \(xx’\) và \(yy’\) cắt nhau tại \(O\) và góc \(xOy\) vuông. Khi đó các góc \(yOx’ ; x’Oy’ ; y’Ox\) cũng đều là những góc vuông. Vì sao ?

Hướng dẫn suy luận:

Sử dụng hai góc kề bù và hai góc đối đỉnh

Lời giải chi tiết

Ta có:

\(\widehat {x'Oy'}\) và \(\widehat {xOy}\) là hai góc đối đỉnh \( \Rightarrow \widehat {x'Oy'} = \widehat {xOy} = {90^o}\)

\(\widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù \( \Rightarrow \)\(\widehat {xOy} + \widehat {xOy'} = {180^o}\)  

\( \Rightarrow \widehat {xOy'} = {180^o} - \widehat {xOy} = {180^o} - {90^o} = {90^o}\)

\(\widehat {xOy'}\) và \(\widehat {x'Oy}\) là hai góc đối đỉnh \( \Rightarrow\widehat {xOy'} = \widehat {x'Oy} = {90^o}\)

Khi đó \(\widehat {x'Oy'};\widehat {xOy'} ; \widehat {x'Oy}\) đều là những góc vuông.

Loigiaihay.com