Lý thuyết trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh(c.g.c)Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. Quảng cáo
1. Định lý Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. Xét tam giác \(ABC\) và tam giác \(A'B'C'\) có: \(\left. {\begin{array}{*{20}{c}}{AB = A'B'}\\{\widehat A = \widehat {A'}}\\{AC = A'C'}\end{array}} \right\} \Rightarrow \Delta ABC = \Delta A'B'C'\left( {c - g - c} \right)\)
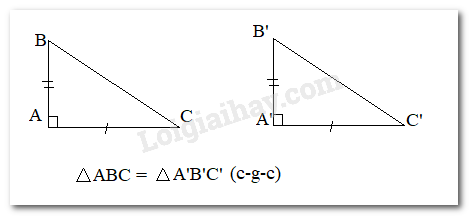
2. Áp dụng vào tam giác vuông * Nếu hai cạnh góc vuông của tam giác này lần lượt bằng hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó bằng nhau.(c-g-c)
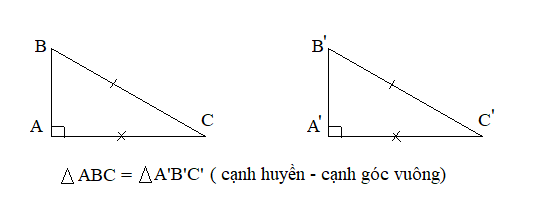
* Nếu cạnh huyền và cạnh góc vuông của tam giác này lần lượt bằng cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác vuông đó bằng nhau.( cạnh huyền - cạnh góc vuông)
3. Các dạng toán thường gặp Dạng 1: Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-góc-cạnh Phương pháp: Sử dụng: “Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.” Hoặc hệ quả: “Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.” Dạng 2: Chứng minh hai đoạn thẳng bằng nhau, các góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc. Phương pháp: + Chọn hai tam giác có các yếu tố cần tính hoặc chứng minh. + Chứng minh hai tam giác bằng nhau theo trường hợp cạnh-góc-cạnh + Suy ra các yếu tố cần thiết để giải bài toán.
|





















Danh sách bình luận