Lý thuyết quy đồng mẫu thức nhiều phân thức1. Tìm mẫu thức chung Quảng cáo
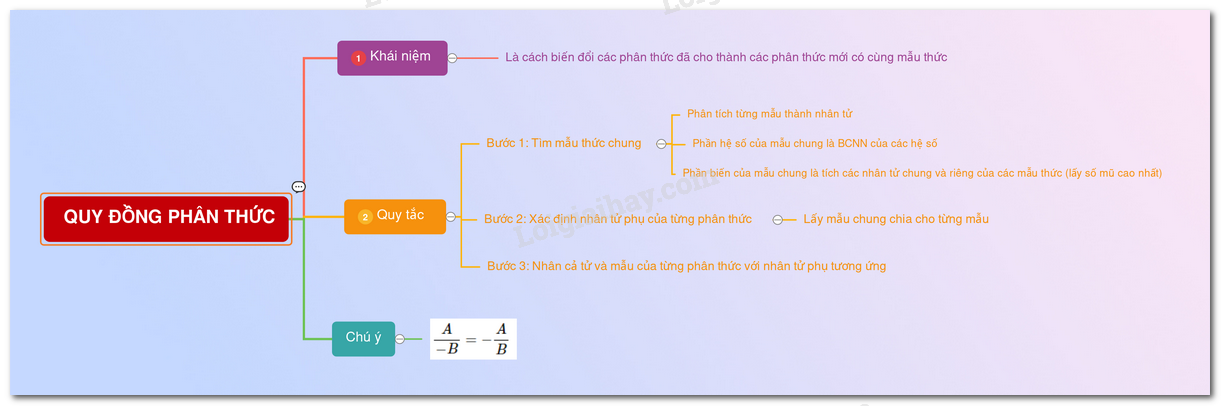
1. Các kiến thức cần nhớ Quy đồng mẫu thức Định nghĩa: Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt các phân thức đã cho. Phương pháp quy đồng mẫu thức nhiều phân thức * Tìm mẫu chung + Phân tích phần hệ số thành thừa số nguyên tố và phần biến thành nhân tử + Mẫu chung bao gồm: phần hệ số là BCNN của các hệ số của mẫu và phần biến là tích giữa các nhân tử chung và riêng mỗi nhân tử lấy số mũ lớn nhất. * Tìm nhân tử phụ mỗi phân thức: Lấy mẫu chung chia cho từng mẫu (đã phân tích thành nhân tử). * Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. Ví dụ: Quy đồng mẫu thức các phân thức \(\dfrac{1}{{{x^3} + 1}};\dfrac{2}{{3x + 3}};\dfrac{x}{{2{x^2} - 2x + 2}}\) Giải: Ta có: \({x^3} + 1 = \left( {x + 1} \right)\left( {{x^2} - x + 1} \right)\); \(3x + 3 = 3\left( {x + 1} \right);\)\(2{x^2} - 2x + 2 = 2\left( {{x^2} - x + 1} \right)\) và BCNN\(\left( {2;3} \right) = 6\) nên các phân thức \(\dfrac{1}{{{x^3} + 1}};\dfrac{2}{{3x + 3}};\dfrac{x}{{2{x^2} - 2x + 2}}\) có mẫu chung là \(6\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = 6\left( {{x^3} + 1} \right).\) * Nên nhân tử phụ của \(\dfrac{1}{{{x^3} + 1}}\) là \(6\) \( \Rightarrow \dfrac{1}{{{x^3} + 1}} = \dfrac{6}{{6\left( {{x^3} + 1} \right)}}\) * Nhân tử phụ của \(\dfrac{2}{{3x + 3}}\) là \(2\left( {{x^2} - x + 1} \right)\) \( \Rightarrow \dfrac{2}{{3x + 3}} = \dfrac{{2.2\left( {{x^2} - x + 1} \right)}}{{3\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \dfrac{{4{x^2} - 4x + 4}}{{6\left( {{x^3} + 1} \right)}}.\) * Nhân tử phụ của \(\dfrac{x}{{2{x^2} - 2x + 2}}\) là \(3\left( {x + 1} \right)\) \( \Rightarrow \dfrac{x}{{2{x^2} - 2x + 2}} = \dfrac{{x.3\left( {x + 1} \right)}}{{2\left( {{x^2} - x + 1} \right).3\left( {x + 1} \right)}} = \dfrac{{3{x^2} + 3x}}{{6\left( {{x^3} + 1} \right)}}.\) Vậy ta được 3 phân thức sau khi qui đồng là: \(\dfrac{6}{{6\left( {{x^3} + 1} \right)}};\dfrac{{4{x^2} - 4x + 4}}{{6\left( {{x^3} + 1} \right)}};\dfrac{{3{x^2} + 3x}}{{6\left( {{x^3} + 1} \right)}}\) 2. Các dạng toán thường gặp Dạng 1: Tìm mẫu thức chung của các phân thức Phương pháp: Để quy đồng mẫu thức nhiều phân thức ta thực hiện các bước sau: * Tìm mẫu chung + Phân tích phần hệ số thành thừa số nguyên tố và phần biến thành nhân tử + Mẫu chung bao gồm: phần hệ số là BCNN của các hệ số của mẫu và phần biến là tích giữa các nhân tử chung và riêng mỗi nhân tử lấy số mũ lớn nhất. * Tìm nhân tử phụ mỗi phân thức: Lấy mẫu chung chia cho từng mẫu (đã phân tích thành nhân tử). * Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
|




















Danh sách bình luận