Lý thuyết Phép nhân và phép chia phân số Toán 6 Chân trời sáng tạo

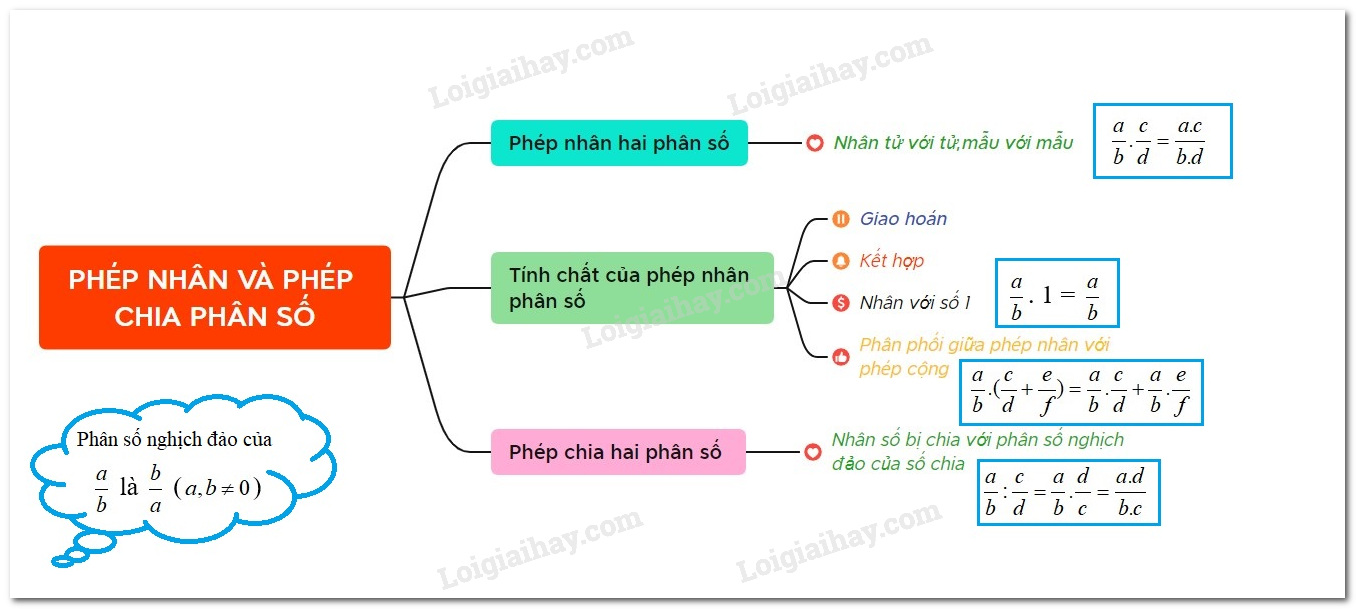
I. Nhân hai phân số

Ví dụ:

a) $\dfrac{{ - 1}}{4}.\dfrac{1}{5} = \dfrac{{\left( { - 1} \right).1}}{{4.5}} = \dfrac{{ - 1}}{{20}}$

b) $2.\dfrac{4}{5} = \dfrac{{2.4}}{5} = \dfrac{8}{5}$.

II. Một số tính chất của phép nhân phân số

Ví dụ:

a) $\dfrac{{ - 3}}{{29}}.\dfrac{9}{{14}}.\dfrac{{ - 29}}{3} = \dfrac{{ - 3}}{{29}}.\dfrac{{ - 29}}{3}.\dfrac{9}{{14}} = \left( {\dfrac{{ - 3}}{{29}}.\dfrac{{ - 29}}{3}} \right).\dfrac{9}{{14}} = 1.\dfrac{9}{{14}} = \dfrac{9}{{14}}$

b)

$\begin{array}{l}\dfrac{7}{{23}}.\dfrac{{24}}{{11}} + \dfrac{7}{{23}}.\dfrac{{ - 2}}{{11}} = \dfrac{7}{{23}}.\left( {\dfrac{{24}}{{11}} + \dfrac{{ - 2}}{{11}}} \right)\\ = \dfrac{7}{{23}}.2 = \dfrac{{14}}{{23}}\end{array}.$

III. Chia phân số

a) Số nghịch đảo

Ví dụ: Số nghịch đảo của $\dfrac{5}{6}$ là $\dfrac{6}{5}$; số nghịch đảo của $ - 5$ là $ - \dfrac{1}{5}$.

b) Qui tắc chia hai phân số

Ví dụ: $\dfrac{{ - 1}}{6}:\dfrac{3}{{13}} = \dfrac{{ - 1}}{6}.\dfrac{{13}}{3} = \dfrac{{\left( { - 1} \right).13}}{{6.3}} = \dfrac{{ - 13}}{{18}}$.

CÁC DẠNG TOÁN VỀ PHÉP NHÂN VÀ PHÉP CHIA PHÂN SỐ

I. Tìm số nghịch đảo của một số cho trước

+ Viết số cho trước dưới dạng $\dfrac{a}{b}\left( {a;b \in Z;a;b \ne 0} \right)$

+ Số nghịch đảo của $\dfrac{a}{b}$ là $\dfrac{b}{a}$

+ Số $0$ không có số nghịch đảo

+ Số nghịch đảo của số nguyên $a{\kern 1pt} \left( {a \ne 0} \right)$ là $\dfrac{1}{a}.$

II. Thực hiện phép nhân, chia phân số

Áp dụng qui tắc chia hai phân số:

Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia.

$\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}}$ ; $a:\dfrac{c}{d} = a.\dfrac{d}{c} = \dfrac{{a.d}}{c}\left( {c \ne 0} \right)$

III. Tìm số chưa biết trong một tích, một thương

+ Muốn tìm một trong hai thừa số, ta lấy tích chia cho thừa số đã biết
+ Muốn tìm số chia, ta lấy số bị chia chia cho thương
+ Muốn tìm số bị chia, ta lấy số chia nhân với thương.

IV. Tính giá trị biểu thức. So sánh giá trị hai biểu thức

- Ta sử dụng các qui tắc cộng, trừ, nhân, chia đã học và chú ý đến thứ tự thực hiện phép tính.
+ Đối với biểu thức không chứa ngoặc ta thực hiện theo thứ tự:

Lũy thừa$ \to $ nhân$ \to $ cộng, trừ

+ Đối với biểu thức có dấu ngoặc ta thực hiện theo thứ tự: $\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}$.

- Để so sánh giá trị hai biểu thức ta thực hiện tính giá trị biểu thức rồi so sánh kết quả.