Lý thuyết mạch có R, L, C mắc nối tiếpLý thuyết mạch có R, L, C mắc nối tiếp. Điện áp và tổng trở của mạch, ... Quảng cáo
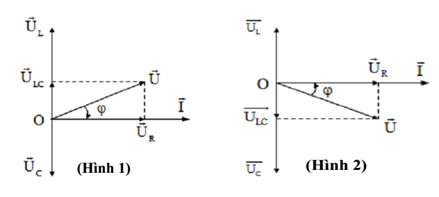
MẠCH CÓ R, L, C MẮC NỐI TIẾP Điện áp và tổng trở của mạch: \(\left\{ \begin{array}{l}U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} \to {U_0} = \sqrt {U_{0R}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} \\Z = \sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \end{array} \right.\) Định luật Ohm cho mạch: \(\left\{ \begin{array}{l}I = \dfrac{U}{Z} = \dfrac{{\sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} }}{{\sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{{U_R}}}{R} = \dfrac{{{U_L}}}{{{Z_L}}} = \dfrac{{{U_C}}}{{{Z_C}}} = \dfrac{{{I_0}}}{{\sqrt 2 }}\\{I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{\sqrt {U_{0R}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} }}{{\sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{{U_{0R}}}}{R} = \dfrac{{{U_{0L}}}}{{{Z_L}}} = \dfrac{{{U_{0C}}}}{{{Z_C}}} = I\sqrt 2 \end{array} \right.\) Độ lệch pha của điện áp và cường độ dòng điện trong mạch là \(\varphi \), được cho bởi: \(\tan \varphi = \dfrac{{{U_L} - {U_C}}}{{{U_R}}} = \dfrac{{{Z_L} - {Z_C}}}{R}\); \(\varphi = {\varphi _u} - {\varphi _i}\) - Khi \(U_L>U_C\) hay \(Z_L>Z_C\) thì u nhanh pha hơn i góc \(\varphi \). (Hình 1). Khi đó ta nói mạch có tính cảm kháng. - Khi \(U_L<U_C\) hay \(Z_L<Z_C\) thì u chậm pha hơn i góc \(\varphi \). (Hình 2). Khi đó ta nói mạch có tính dung kháng. Giản đồ véc tơ (Giản đồ Frenen): Hiện tượng cộng hưởng Khi \({Z_L} = {Z_C} \Leftrightarrow \omega L = \frac{1}{{\omega C}} \Leftrightarrow {\omega ^2}LC = 1\) thì \(\tan \varphi = 0 \Rightarrow \varphi = 0\) suy ta dòng điện i cùng pha với điện áp u. Khi đó: \(\left\{ \begin{array}{l}{Z_{\min }} = R\\{I_{\max }} = \frac{U}{R}\end{array} \right.\) => Đó là hiện tượng cộng hưởng. Sơ đồ tư duy về mạch R, L, C mắc nối tiếp - Vật lí 12
|




















Danh sách bình luận