Lý thuyết hàm số bậc hai

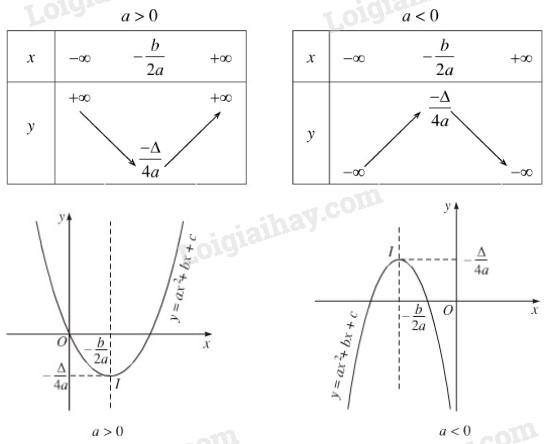
1. Hàm số bậc hai

Định nghĩa

Hàm số bậc hai được cho bởi công thức:

$$y = ax^2 + bx + c (a ≠ 0)$$

có tập xác định $D =\mathbb R$ và biệt thức $\Delta  = {b^2} - 4ac$

Chiều biến thiên:

Nếu $a > 0$ thì hàm số $y = a{x^2} + bx + c$:

+) Nghịch biến trên khoảng $\left( { - \infty ; - \dfrac{b}{{2a}}} \right)$

+) Đồng biến trên khoảng $\left( { - \dfrac{b}{{2a}}; + \infty } \right)$

Hàm số đạt có điểm cực tiểu là $\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)$

Nếu $a < 0$ thì hàm số $y = a{x^2} + bx + c$:

+) Đồng biến trên khoảng $\left( { - \infty ; - \dfrac{b}{{2a}}} \right)$

+) Nghịch biến trên khoảng $\left( { - \dfrac{b}{{2a}}; + \infty } \right)$

Hàm số đạt có điểm cực đại là $\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)$

Bảng biến thiên:

2. Đồ thị hàm số bậc hai

Đồ thị hàm số $y = ax^2+ bx + c (a ≠ 0)$ là đường parabol có:

+) đỉnh là điểm $I\left( { - \dfrac{b}{2a}; - \dfrac{\Delta }{4a}} \right)$

+) trục đối xứng là đường thẳng $x =  - \dfrac{b}{2a}$.

+) Bề lõm của Parabol quay lên trên nếu $a > 0$ và xuống dưới nếu $a < 0$.

+) Giao điểm với trục tung: $A(0; c)$.

+) Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình $ax^2 + bx + c = 0$.

* Cách vẽ

Cách 1: (Dùng cho mọi trường hợp)

Bước 1: Xác định tọa độ đỉnh I

Bước 2: Vẽ trục đối xứng

Bước 3: Xác định tọa độ các giao điểm của Parabol cới trục tung và trục hoành (nếu có)

Bước 4: Vẽ parabol (lưu ý dấu của hệ số a - liên quan đến bề lõm của Parabol)

Cách 2: (sử dụng khi đã có đồ thị hàm số $y = ax^2$)

Đồ thị hàm số $y = ax^2 + bx + c (a ≠ 0)$ suy ra từ đồ thị hàm số $y = ax^2$ bằng cách:

+ Tịnh tiến song song với trục hoành $\left| \dfrac{b}{2a} \right|$ đơn vị về bên trái nếu $\dfrac{b}{2a}$  > 0, về bên phải nếu $\dfrac{b}{2a}$ < 0.

+ Tịnh tiến song song với trục tung $\left|  -  \dfrac{\Delta }{4a} \right|$ đơn vị lên trên nếu $-  \dfrac{\Delta }{4a}$ > 0, và xuống dưới nếu $-  \dfrac{\Delta }{4a}$ < 0.

Loigiaihay.com