Lý thuyết góc và cung lượng giác

1. Đơn vị đo góc và cung tròn

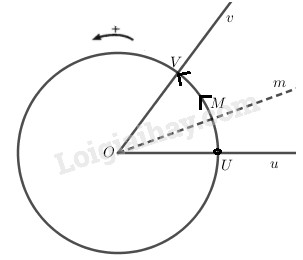
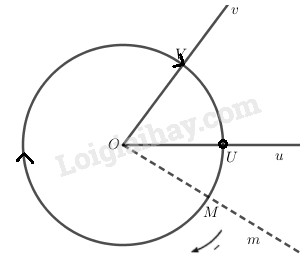
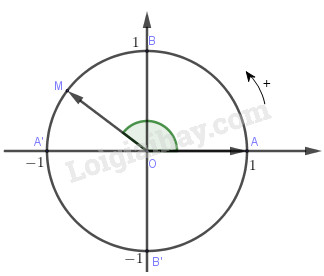
a) Độ là số đo của góc bằng \({1 \over {180}}\) góc bẹt

Số đo của một cung tròn bằng số đo của góc ở tâm chắn cung đo.

Như vậy số đo của cung bằng \({1 \over {180}}\) nửa đường tròn là một độ.

Kí hiệu \(1^0\) đọc là một độ 

\(1^0= 60'\);    \(1' = 60''\)

b) Radian

Cung có độ dài bằng bán kính đường tròn chứa cung ấy có số đo là \(1\) radian, kí hiệu \(1rad \) hay đơn giản là bỏ chữ \(rad\) và kí hiệu là \(1\).

c) Quan hệ giữa độ và radian

\({180^0} = \pi rad \)\(\Rightarrow {1^0} = {\pi  \over {180}}rad,1rad = {\left( {{{180} \over \pi }} \right)^0}\)

d) Độ dài cung tròn

Một cung của đường tròn bán kính \(R\) có số đo \(α\) \( rad\) thì độ dài \(l = Rα\).

2. Góc và cung lượng giác

- Đường tròn định hướng là đường tròn có chiều di động đã được quy ước: chiều dương là ngược chiều kim đồng hồ, chiều âm là cùng chiều đồng hồ.

Chú ý: Ta chỉ xét các khái niệm góc lượng giác, cung lượng giác trên đường tròn định hướng.

- Góc lượng giác: Khi tia \(Om\) quay chỉ theo chiều dương hoặc chỉ theo chiều âm từ tia \(Ou\) đến tia \(Ov\) thì nó quét một góc lượng giác với tia đầu \(Ou\) và tia cuối \(Ov\), kí hiệu \(\left( {Ou,Ov} \right)\).

- Cung lượng giác: Khi tia \(Om\) quét nên một góc lượng giác \(\left( {Ou,Ov} \right)\) thì điểm \(M\) chạy trên đường tròn luôn theo một chiều dương hoặc âm từ \(U\) đến \(V\). Ta nói điểm \(M\) vạch nên một cung lượng giác điểm đầu \(U\) và điểm cuối \(V\) tương ứng với góc lượng giác \(\left( {Ou,Ov} \right)\).

- Số đo góc và cung lượng giác

- Nếu một góc lượng giác có số đo \({a^0}\) (hay \(\alpha \left( {rad} \right)\)) thì mọi góc lượng giác cùng tia đầu, tia cuối với nó có số đo dạng \({a^0} + k{360^0}\) (hay \(\alpha  + k2\pi \left( {rad} \right)\)), \(k \in Z\).

Chú ý: Không viết \({a^0} + k2\pi \) hay \(\alpha  + k{360^0}\) (vì không cùng đơn vị đo).

- Nếu một cung lượng giác có số đo \({a^0}\) (hay \(\alpha \left( {rad} \right)\)) thì mọi góc lượng giác cùng tia đầu, tia cuối với nó có số đo dạng \({a^0} + k{360^0}\) (hay \(\alpha  + k2\pi \left( {rad} \right)\)), \(k \in Z\).

3. Hệ thức Salơ

Ba tia chung gốc \(OA, OB, OC\) bất kì thì:

\(sđ(OA, OB) + sđ(OB, OC) \)\(= sđ(OA, OC) + k.360^0\) \((k2π)\)

4. Biểu diễn cung lượng giác trên đường tròn lượng giác

a) Đường tròn lượng giác là đường tròn định hướng có tâm là gốc \(O\) của hệ toạ độ trực chuẩn có bán kính bằng 1. Điểm gốc của cung lượng giác là điểm \(A (1; 0)\)

b) Biểu diễn cung lượng giác trên đường tròn lượng giác có số đo bằng \(α\) bằng cách chọn điểm gốc là điểm \(A(1;0)\) là điểm ngọn \(M\) sao cho sđ cung \(AM\) bằng \(α\).  

Loigiaihay.com