Lý thuyết giao thoa ánh sáng

Lý thuyết giao thoa ánh sáng

1. HIỆN TƯỢNG NHIỄU XẠ ÁNH SÁNG

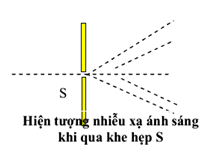- Đối với ánh sáng đơn sắc: được đặc trưng bởi tần số f:

f_đỏ ≠ f_tím  \( \to \lambda  = \dfrac{c}{f}\)

- Khi ánh sáng qua mặt phân cách giữa hai môi trường thì: f - không đổi

\( \to \lambda ' = \dfrac{v}{f} = \dfrac{v}{{\dfrac{c}{{{\lambda _{ck}}}}}} = \dfrac{{{\lambda _{ck}}}}{n}\)

2. GIAO THOA ÁNH SÁNG

- Thí nghiệm của I-âng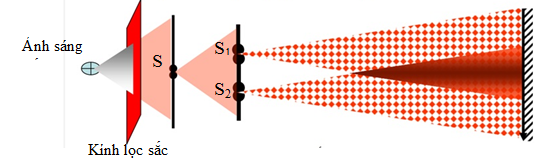

+ Giải thích: S đóng vai trò là một nguồn phát sóng truyền tới S₁, S₂ khi đó, S₁S₂ là hai nguồn phát sóng kết hợp (cùng tần số và có độ lệch pha không đổi)

+ Kết luận: Hiện tượng giao thoa ánh sáng là bằng chứng thực nghiệm khẳng định ánh sáng có tính chất sóng.

- Vị trí các vân giao thoa - khoảng vân

Xét TN I-âng, với khoảng S₁S₂ = a, S₁E = D, Bước sóng ánh sáng đơn sắc λ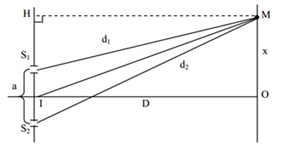

\(\left\{ \begin{array}{l}OM = x\\{d_2} - {d_1} = \dfrac{{{\rm{2ax}}}}{{{d_1} + {d_2}}}\end{array} \right.\)  Xét \(x \ll D, \to \left\{ \begin{array}{l}{d_1} + {d_2} = 2D\\{d_2} - {d_1} = \dfrac{{{\rm{ax}}}}{D}\end{array} \right.\)

• Nếu tại M ℓà vân sáng \( \to {d_2} - {d_1} = k\lambda \) với k ℓà vân sáng bậc k \(k \in \left( {0;{\rm{ }} \pm {\rm{ }}1;{\rm{ }} \pm {\rm{ }}2;{\rm{ }} \ldots } \right)\)
• Nếu tại M ℓà vân tối $ \to {d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda $ với k ℓà vân tối thứ (k + 1) \(k \in \left( {0;{\rm{ }} \pm {\rm{ }}1;{\rm{ }} \pm {\rm{ }}2 \ldots } \right)\)

+ Vị trí vân sáng: \({d_2} - {\rm{ }}{d_1} = \dfrac{{{\rm{ax}}}}{D} = k\lambda  \to {x_s} = k\dfrac{{\lambda D}}{a}\)

Trong đó: k ℓà vân sáng bậc k (k = 0, ± 1, ± 2, ± 3….)

Chú ý: k = 0 là vân sáng trung tâm

+ Vị trí vân tối: \({d_2} - {\rm{ }}{d_1} = \dfrac{{{\rm{ax}}}}{D} = \left( {k + \dfrac{1}{2}} \right)\lambda \to {x_t} = \left( {k + \dfrac{1}{2}} \right)\dfrac{{\lambda D}}{a}\)

Trong đó (k = 0, ± 1, ± 2, ± 3 …).

      - Nếu k > 0: thì k ℓà vân tối thứ (k + 1)

      - Nếu k < 0 thì k ℓà vân tối thứ (-k)

+ Khoảng vân i: ℓà khoảng cách giữa hai vân sáng hoặc hai vân tối ℓiên tiếp:

\(i = \dfrac{{\lambda D}}{a}\)   

\( \to {x_s} = ki;{x_t} = \left( {k + \dfrac{1}{2}} \right)i\)

Trong đó:

• \(\lambda \) là bước sóng ánh sáng (m)
• D là khoảng cách từ mặt phẳng S₁S₂ đến màn M
• a là khoảng cách giữa hai khe S₁S₂

+ Ứng dụng: Đo bước sóng ánh sáng \(\lambda = \dfrac{{ai}}{D}\)

+ Giữa $N$ vân sáng liên tiếp có $(N-1)$ khoảng vân

+ Khoảng cách từ vân sáng đến vân tối là $i/2$

+ Vân tối thứ $k$ nằm giữa vân sáng thứ k và $(k-1)$

+ Khi nhúng vào nước, khoảng vân giảm $n$ lần so với khi đặt ngoài không khí: \(i' = \dfrac{i}{n}\) ($n$ chiết suất tuyệt đối của nước)

Video mô phỏng về vân giao thoa

Sơ đồ tư duy về giao thoa ánh sáng - Vật lí 12